题目内容
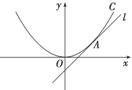
如图，直线l：y＝x＋b与抛物线C：x2＝4y相切于点A.
(1)求实数b的值；
(2)求以点A为圆心，且与抛物线C的准线相切的圆的方程．
解：(1)由
得x2－4x－4b＝0.(*)
因为直线l与抛物线C相切，所以Δ＝(－4)2－4×(－4b)＝0，解得b＝－1.
(2)由(1)可知b＝－1，故方程(*)即为x2－4x＋4＝0，
解得x＝2.将其代入x2＝4y，得y＝1.
故点A(2,1)．
因为圆A与抛物线C的准线相切，
所以圆A的半径r等于圆心A到抛物线的准线y＝－1的距离，
即r＝|1－(－1)|＝2，
所以圆A的方程为(x－2)2＋(y－1)2＝4.
练习册系列答案
53天天练系列答案
相关题目
＝－
，求直线l的方程；
圆的离心率的比值是( )
D.
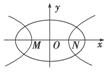
中，椭圆C的中心为原点，焦点F1，F2在x轴上，离心率为
.过F1的直线l交C于A，B两点，且△ABF2的周长为16，那么C的方程为________________．
1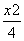
＋
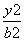＝1(0＜b＜2)的离心率为
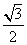，抛物线C2：x2＝2py(p＞0)的焦点是椭圆的顶点．
(－1,0)，B(1,0)，则顶点C的轨迹方程为________．
＋
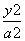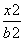＝1(a>b>0)上的两点
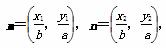，且
m·n＝0，椭圆离心率e＝
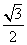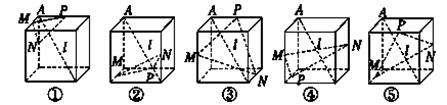
，短轴长为2，O为坐标原点．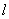
是正方体的一条体对角线，点M、N、P分别为其所在棱的中点，能得出