题目内容
14.执行如图所示的程序框图,则输出S的值为( )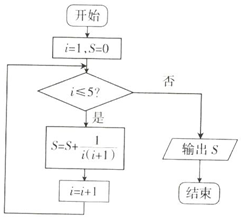
| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{7}$ | D. | $\frac{7}{8}$ |
分析 模拟程序的运行,可得程序框图的功能是计算并输出S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{5×6}$的值,由裂项法即可计算得解.
解答 解:模拟程序的运行,可得程序框图的功能是计算并输出S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{5×6}$的值,
S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{5×6}$=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+…+($\frac{1}{5}$-$\frac{1}{6}$)=1-$\frac{1}{6}$=$\frac{5}{6}$.
故选:A.
点评 本题主要考查了循环结构的程序框图的应用,模拟程序的运行得到程序框图的功能是解题的关键,属于基础题.

练习册系列答案
相关题目
2.已知一个三棱锥的三视图如图所示,则该三棱锥的体积( )


| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
9.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分.两人4局的得分情况如下:
(1)已知在乙的4局比赛中随机选取1局时,此局得分小于6分的概率不为零,且在4局比赛中,乙的平均得分高于甲的平均得分,求x+y的值;
(2)如果x=6,y=10,从甲、乙两人的4局比赛中随机各选取1局,并将其得分分别记为a,b,求a>b的概率;
(3)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出x的所有可能取值.(结论不要求证明)
| 甲 | 6 | 6 | 9 | 9 |
| 乙 | 7 | 9 | x | y |
(2)如果x=6,y=10,从甲、乙两人的4局比赛中随机各选取1局,并将其得分分别记为a,b,求a>b的概率;
(3)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出x的所有可能取值.(结论不要求证明)
19.已知函数f(x)=e|ln2x|-|x-$\frac{1}{4x}$|,若f(x1)=f(x2)且x1≠x2,则下面结论正确的是( )
| A. | x1+x2-1>0 | B. | x1+x2-1<0 | C. | x2-x1>0 | D. | x2-x1<0 |
6.如图所示,若a=-4,则输出结果是( )


| A. | 是正数 | B. | 是负数 | C. | -4 | D. | 16 |
3.某程序框图如图所示,则该程序运行后输出的B=( )


| A. | 15 | B. | 29 | C. | 31 | D. | 63 |
4.如果满足不等式$|{x-\frac{5}{4}}|<b({b>0})$的一切实数x也满足不等式|x-1|<$\frac{1}{2}$,则b的取值范围是( )
| A. | $({0,\frac{3}{4}})$ | B. | $({0,\frac{1}{4}}]$ | C. | $[{\frac{1}{4},\frac{3}{4}}]$ | D. | $[{\frac{3}{4},+∞})$ |