题目内容
在平面直角坐标系xOy中,已知椭圆C:
+
=1(a>b>0)的离心率为
.且过点(3,-1).
(1)求椭圆C的方徎;
(2)若动点P在直线l:x=-2
上,过P作直线交椭圆C于M,N两点,使得PM=PN,再过P作直线l′⊥MN,直线l′是否恒过定点,若是,请求出该定点的坐标;若否,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
(1)求椭圆C的方徎;
(2)若动点P在直线l:x=-2
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
,同此能求出椭圆C的方程.
(2)直线l的方程为x=-2
,设P(-2
,y0),y0∈(-
,
),当y0≠0时,设M(x1,y1),N(x2,y2),由题意知x1≠x2,利用点差法l′的方程为y=-
(x+
),从而得到l′恒过定点(-
,0).当y0=0时,直线MN为x=-2
,由此推导出l′恒过定点(-
,0).
|
(2)直线l的方程为x=-2
| 2 |
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
| 3y0 | ||
2
|
4
| ||
| 3 |
4
| ||
| 3 |
| 2 |
4
| ||
| 3 |
解答:
解:(1)∵椭圆C:
+
=1(a>b>0)的离心率为
.且过点(3,-1),
∴
,
解得a2=12,b2=4,
∴椭圆C的方程为
+
=1.
(2)∵直线l的方程为x=-2
,
设P(-2
,y0),y0∈(-
,
),
当y0≠0时,设M(x1,y1),N(x2,y2),由题意知x1≠x2,
联立
,
∴
+
=0,
∴
=-
•
,
又∵PM=PN,∴P为线段MN的中点,
∴直线MN的斜率为-
•
=
,
又l′⊥MN,∴l′的方程为y-y0=-
(x+2
),
即y=-
(x+
),
∴l′恒过定点(-
,0).
当y0=0时,直线MN为x=-2
,
此时l′为x轴,也过点(-
,0),
综上,l′恒过定点(-
,0).
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
∴
|
解得a2=12,b2=4,
∴椭圆C的方程为
| x2 |
| 12 |
| y2 |
| 4 |
(2)∵直线l的方程为x=-2
| 2 |
设P(-2
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
当y0≠0时,设M(x1,y1),N(x2,y2),由题意知x1≠x2,
联立
|
∴
| x12-x22 |
| 12 |
| y12-y22 |
| 4 |
∴
| y1-y2 |
| x1-x2 |
| 1 |
| 3 |
| x1+x2 |
| y1+y2 |
又∵PM=PN,∴P为线段MN的中点,
∴直线MN的斜率为-
| 1 |
| 3 |
-2
| ||
| y0 |
2
| ||
| 3y0 |
又l′⊥MN,∴l′的方程为y-y0=-
| 3y0 | ||
2
|
| 2 |
即y=-
| 3y0 | ||
2
|
4
| ||
| 3 |
∴l′恒过定点(-
4
| ||
| 3 |
当y0=0时,直线MN为x=-2
| 2 |
此时l′为x轴,也过点(-
4
| ||
| 3 |
综上,l′恒过定点(-
4
| ||
| 3 |
点评:本题考查椭圆方程的求法,考查直线是否恒过定点的判断与求法,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
如果复数
(其中b∈R)的实部与虚部互为相反数,则b=( )
| 2-bi |
| i3 |
| A、2 | B、-2 | C、-1 | D、1 |
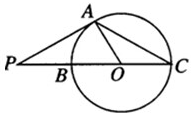 如图,已知P是圆O外一点,PA为圆O的切线,A为切点.割线PBC经过圆心O,若PA=3
如图,已知P是圆O外一点,PA为圆O的切线,A为切点.割线PBC经过圆心O,若PA=3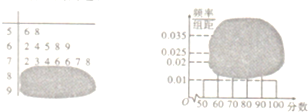 某高校自主招生面试成绩的茎叶图和频率分布直方图均受到不同程度的破坏,其可见部分信息如图所示,据此解答下列问题;
某高校自主招生面试成绩的茎叶图和频率分布直方图均受到不同程度的破坏,其可见部分信息如图所示,据此解答下列问题;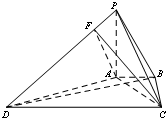 如图,在四棱锥P-ABCD中,已知AB=1,BC=2,CD=4,AB∥CD,BC⊥CD,平面PAB⊥平面ABCD,PA⊥AB.
如图,在四棱锥P-ABCD中,已知AB=1,BC=2,CD=4,AB∥CD,BC⊥CD,平面PAB⊥平面ABCD,PA⊥AB.