题目内容
1．曲线y=x3+2x+1在点P（1，4）处的切线与y轴交点的纵坐标是（ ）| A． | -9 | B． | -3 | C． | -1 | D． | 3 |
分析 求出函数的导数，可得切线的斜率，由点斜式方程可得切线方程，再令x=0，即可得到所求纵坐标．
解答 解：y=x3+2x+1的导数为y′=3x2+2，
可得在点P（1，4）处的切线斜率为3+2=5，
曲线在点P（1，4）处的切线方程为y-4=5（x-1），
令x=0，可得y=4-5=-1．
故选：C．
点评 本题考查导数的运用：求切线的方程，正确求导和运用点斜式方程是解题的关键，考查运算能力，属于基础题．
练习册系列答案
相关题目
12．计算sin75°cos15°-cos75°sin15°的值等于（ ）
| A． | 0 | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
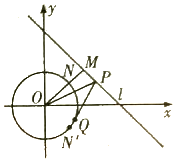已知圆O：x2+y2=2，直线l过点$M（\frac{3}{2}，\frac{3}{2}）$，且OM⊥l，P（x0，y0）是直线l上的动点，线段OM与圆O的交点为点N，N'是N关于x轴的对称点．
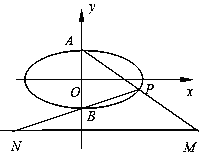如图，已知椭圆$C：\frac{x^2}{4}+{y^2}=1$的上、下顶点分别为A，B，点P在椭圆上，且异于点A，B，直线AP，BP与直线l：y=-2分别交于点M，N，