题目内容
15.已知命题p:x2+2x-3>0;命题q:$\frac{1}{3-x}$>1,若“(¬q)∧p”为真,求x的取值范围.分析 根据不等式的解法求出命题的等价条件,结合复合命题真假关系进行求解即可.
解答 解:由x2+2x-3>0得x>1或x<-3,即p:x>1或x<-3,
由$\frac{1}{3-x}$>1得$\left\{\begin{array}{l}{3-x>0}\\{1>3-x}\end{array}\right.$,即$\left\{\begin{array}{l}{x<3}\\{x>2}\end{array}\right.$,则2<x<3,
即q:2<x<3,¬q:x≥3或x≤2,
若“(¬q)∧p”为真,
则$\left\{\begin{array}{l}{x>1或x<-3}\\{x≥3或x≤2}\end{array}\right.$,得x≥3或1<x≤2或x<-3,
即x的取值范围是x≥3或1<x≤2或x<-3.
点评 本题主要考查复合命题真假关系的判断,根据不等式的解法求出命题的等价条件是解决本题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
6.已知集合A={1,2,3,5},B={x|x-2>0},那么集合A∩B等于( )
| A. | {1} | B. | {3} | C. | {1,3} | D. | {3,5} |
10.已知命题p:“?x0∈R,e${\;}^{{x}_{0}}$-x0-1≤0”,则¬p为( )
| A. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≥0 | B. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1>0 | ||
| C. | ?x∈R,ex-x-1>0 | D. | ?x∈R,ex-x-1≥0 |
20.已知平面区域D={(x,y)|$\left\{\begin{array}{l}{x-4y+3≤0}\\{3x+5y-25≤0}\\{x≥1}\end{array}\right.$},Z=$\frac{y}{x+2}$.若命题“?(x,y)∈D,Z≥m”为真命题,则实数m的最大值为( )
| A. | $\frac{22}{15}$ | B. | $\frac{2}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
7.设全集U=R,集合A={x|x≥2},B={x|0≤x<6},则集合(∁UA)∩B=( )
| A. | {x|0<x<2} | B. | {x|0<x≤2} | C. | {x|0≤x<2} | D. | {x|0≤x≤2} |
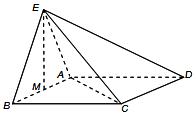 如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.
如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.