题目内容
若函数f(x)在给定区间M上存在的正数t,使得对任意的x∈M,有x+t∈M,且f(x+t)≥f(x),则称f(x)为M上的t级类增函数,给出下列命题:
①函数f(x)=3x是R上的1级类增函数;
②若函数f(x)=R上单调递增,则f(x)一定为R上的t级类增函数;
③若函数f(x)=sinx+ax为[
,+∞]上的
级类增函数,则实数a的最小值为2;
④若函数f(x)=x2-3x为[1,+∞)上的t级类增函数,则实数t的取值范围为[1,+∞).
其中正确的命题为 (写出所有正确命题的序号).
①函数f(x)=3x是R上的1级类增函数;
②若函数f(x)=R上单调递增,则f(x)一定为R上的t级类增函数;
③若函数f(x)=sinx+ax为[
| π |
| 2 |
| π |
| 3 |
④若函数f(x)=x2-3x为[1,+∞)上的t级类增函数,则实数t的取值范围为[1,+∞).
其中正确的命题为
考点:进行简单的合情推理
专题:综合题,推理和证明
分析:①f(x+1)-f(x)=3x+1-3x=2•3x;
②x+t>x,f(x+t)>f(x)恒成立,即可判断;
③函数f(x)=sinx+ax为[
,+∞]上的
级类增函数,故运用参数分离,求出最大值,只要a不小于最大值即可;
④由f(x)=x2-3x为[1,+∞)上的t级类增函数,能导出实数t的取值范围为[1,+∞).
②x+t>x,f(x+t)>f(x)恒成立,即可判断;
③函数f(x)=sinx+ax为[
| π |
| 2 |
| π |
| 3 |
④由f(x)=x2-3x为[1,+∞)上的t级类增函数,能导出实数t的取值范围为[1,+∞).
解答:
解:对于①,函数f(x)=3x,∴f(x+1)-f(x)=3x+1-3x=2•3x,∴3x≥0在(-∞,+∞)上恒成立,∴①正确;
对于②,∵x+t>x,∴f(x+t)>f(x)恒成立,∴②正确;
对于③,f(x)=sinx+ax为[
,+∞]上的
级类增函数,∴sin(x+
)+a(x+
)≥sinx+ax,sinxcos
+cosxsin
+ax+
a≥sinx+ax,∴
cosx+
a≥
sinx,当x=
时,
a≥
,a≥
,∴则实数a的最小值为2,∴③不正确;
对于④,∵f(x)=x2-3x为[1,+∞)上的t级类增函数,∴(x+t)2-3(x+t)≥x2-3x,
∴2tx+t2-3t≥0,t≥3-2x,由于x∈[1,+∞),则3-2x≤1,故实数t的取值范围为[1,+∞),∴④正确.
故答案为:①②④.
对于②,∵x+t>x,∴f(x+t)>f(x)恒成立,∴②正确;
对于③,f(x)=sinx+ax为[
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| 3 |
| 2π |
对于④,∵f(x)=x2-3x为[1,+∞)上的t级类增函数,∴(x+t)2-3(x+t)≥x2-3x,
∴2tx+t2-3t≥0,t≥3-2x,由于x∈[1,+∞),则3-2x≤1,故实数t的取值范围为[1,+∞),∴④正确.
故答案为:①②④.
点评:本题考查命题的真假判断,考查新定义,同时考查函数的性质及应用,是中档题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某项活动从甲、乙、丙、丁四人中任选两名参加,甲被选中的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知两点A(-1,0),B(0,1),点P是圆C:(x-1)2+y2=1上任意一点,则点P到直线AB的距离d的最大值与最小值分别是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
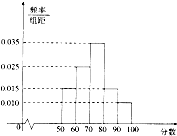 某中学组织全校340名学生参加消防知识竞赛,成绩如图所示,其中得分在区间[90,100]内的人数为
某中学组织全校340名学生参加消防知识竞赛,成绩如图所示,其中得分在区间[90,100]内的人数为