题目内容
2.若实数x,y满足条件$\left\{\begin{array}{l}{x≥1}\\{x-2y+3≥0}\\{y≥x}\end{array}\right.$,则z=$\frac{y}{x+1}$的最小值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
分析 作出约束条件的平面区域,易知z=$\frac{y}{x+1}$的几何意义是点A(x,y)与点D(-1,0)连线的直线的斜率,从而解得.
解答 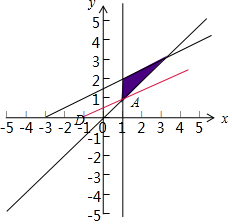 解:由题意作实数x,y满足条件$\left\{\begin{array}{l}{x≥1}\\{x-2y+3≥0}\\{y≥x}\end{array}\right.$的平面区域如下,
解:由题意作实数x,y满足条件$\left\{\begin{array}{l}{x≥1}\\{x-2y+3≥0}\\{y≥x}\end{array}\right.$的平面区域如下,
z=$\frac{y}{x+1}$的几何意义是点P(x,y)与点D(-1,0),连线的直线的斜率,由$\left\{\begin{array}{l}{x=1}\\{y=x}\end{array}\right.$,解得A(1,1)
故当P在A时,z=$\frac{y}{x+1}$有最小值,
z=$\frac{y}{x+1}$=$\frac{1}{2}$.
故选:B.
点评 本题考查了平面向量的应用及数形结合的思想应用,同时考查了斜率公式的应用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
12.已知集合A={x|x≥3或x≤-1},B={x|=-2≤x≤2},则A?B=( )
| A. | [-2,-1] | B. | [-1,2) | C. | [-1,1] | D. | [1,2) |
10.sin4cos3tan2的值为( )
| A. | 负数 | B. | 正数 | C. | 0 | D. | 不存在 |
7.已知角α的顶点在原点,始边与x轴的正半轴重合
(1)若终边经过点P(-1,2),求sin αcos α的值;
(2)若角α的终边在直线y=-3x上,求tan α+$\frac{3}{cosα}$的值.
(1)若终边经过点P(-1,2),求sin αcos α的值;
(2)若角α的终边在直线y=-3x上,求tan α+$\frac{3}{cosα}$的值.
12.若曲线${C_1}:{x^2}+{y^2}-2x=0$与曲线${C_2}:m{x^2}-xy+mx=0$有三个不同的公共点,则实数m的取值范围是( )
| A. | $(0,\sqrt{3})$ | B. | $(-\sqrt{3},0)∪(0,\sqrt{3})$ | C. | $(0,\frac{{\sqrt{3}}}{3})$ | D. | $(-\frac{{\sqrt{3}}}{3},0)∪(0,\frac{{\sqrt{3}}}{3})$ |