题目内容
12.若曲线${C_1}:{x^2}+{y^2}-2x=0$与曲线${C_2}:m{x^2}-xy+mx=0$有三个不同的公共点,则实数m的取值范围是( )| A. | $(0,\sqrt{3})$ | B. | $(-\sqrt{3},0)∪(0,\sqrt{3})$ | C. | $(0,\frac{{\sqrt{3}}}{3})$ | D. | $(-\frac{{\sqrt{3}}}{3},0)∪(0,\frac{{\sqrt{3}}}{3})$ |
分析 把圆的方程化为标准方程,求出圆心和半径,直线过定点(-1,0),当直线mx-y+m=0与圆相切时,根据圆心到直线的距离d=$\frac{2|m|}{\sqrt{{m}^{2}+1}}$=r=1,求出m的值,数形结合求出实数m的取值范围.
解答 解:由题意可知曲线C1:x2+y2-2x=0表示一个圆,化为标准方程得: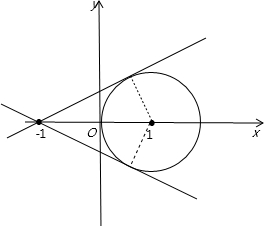
(x-1)2+y2=1,所以圆心坐标为(1,0),半径r=1;
${C_2}:m{x^2}-xy+mx=0$表示两条直线x=0和mx-y+m=0,
由直线mx-y+m=0可知:此直线过定点(-1,0),
在平面直角坐标系中画出图象如图所示:
当直线mx-y+m=0与圆相切时,
圆心到直线的距离d=$\frac{2|m|}{\sqrt{{m}^{2}+1}}$=r=1,
化简得:m=±$\frac{\sqrt{3}}{3}$.
则直线y-mx-m=0与圆相交时,m∈(-$\frac{\sqrt{3}}{3}$,0)∪(0,$\frac{\sqrt{3}}{3}$),
故选D.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
2.若实数x,y满足条件$\left\{\begin{array}{l}{x≥1}\\{x-2y+3≥0}\\{y≥x}\end{array}\right.$,则z=$\frac{y}{x+1}$的最小值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
20.在复平面内,复数i(i-1)对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.设F1,F2分别为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)双曲线a≥1的左、右焦点,双曲线上存在一点P使得(|PF1|-|PF2|)2=b2-3ab,则该双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{15}$ | C. | 4 | D. | $\sqrt{17}$ |
4.随着我国经济的发展,居民的储蓄款逐年增长,设某地区城乡居民人民币储蓄存款(年底余额)如表:
(1)取y关于t的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$t+a;
(2)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(2)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.
2.函数f(x)=$\frac{2sinx•cosx}{1+sinx+cosx}$,x∈(0,$\frac{π}{2}$]的最大值M,最小值为N,则M-N=( )
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\sqrt{2}$-1 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$+1 |