题目内容
已知双曲线
-
=1（a＞
）的两条渐近线的夹角为
，则双曲线的离心率的值是 ．
| x2 |
| a2 |
| y2 |
| 2 |
| 2 |
| π |
| 3 |
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：可得双曲线的两条渐近线的倾斜角为30°和150°或60°和120°，结合c2=a2+b2可得．
解答：
解：由题意知双曲线的两条渐近线的夹角为
，且a＞
，
则双曲线的两条渐近线的倾斜角为30°和150°
∵若双曲线的焦点在x轴上，则
=
，
∵c2=a2+b2，∴
=
，
∴e2-1=
，解得e=
，
故答案为：
| π |
| 3 |
| 2 |
则双曲线的两条渐近线的倾斜角为30°和150°
∵若双曲线的焦点在x轴上，则
| b |
| a |
| ||
| 3 |
∵c2=a2+b2，∴
| c2-a2 |
| a2 |
| 1 |
| 3 |
∴e2-1=
| 1 |
| 3 |
2
| ||
| 3 |
故答案为：
2
| ||
| 3 |
点评：本题考查双曲线的几何性质，由渐近线的斜率推导双曲线的离心率是解决本题的关键，属中档题．
练习册系列答案
相关题目
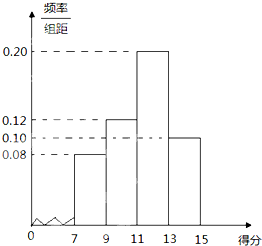某中学高三年级共有学生1000人参加期中考试，今随机抽取50人，对本次考试数学卷第20题的得分情况进行统计，其频率分布直方图如图，在本年级中估计该题得分不低于11分的学生人数有