题目内容
已知各项不为0的等差数列{an}满足a4－2a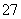
＋3a8＝0，数列{bn}是等比数列，且b7＝a7，则b2b12等于( )
A．1 B．2
C．4 D．8
C
[解析] ∵a4－2a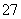＋3a8＝0，∴2a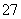＝a4＋3a8＝a7－3d＋3(a7＋d)＝4a7，∴a7＝2，∴b7＝2.
∴b2b12＝b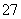＝4，故选C.
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
全能练考卷系列答案一课一练课时达标系列答案题目内容
已知各项不为0的等差数列{an}满足a4－2a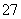＋3a8＝0，数列{bn}是等比数列，且b7＝a7，则b2b12等于( )
A．1 B．2
C．4 D．8
C
[解析] ∵a4－2a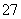＋3a8＝0，∴2a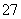＝a4＋3a8＝a7－3d＋3(a7＋d)＝4a7，∴a7＝2，∴b7＝2.
∴b2b12＝b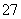＝4，故选C.
全能练考卷系列答案一课一练课时达标系列答案
满足
,则
=_________。
中，已知
，试求n的值 
B．e2 C．e D.
g(x0)成立？如果存在，求出符合条件的一个x0；否则说明理由．
，AB⊥AD，且AE⊥平面ABD，平面CBD⊥平面ABD.
＋5cos2
＝4，则tan C的最大值为( )
B．－
C．－
D．－2