Question

已知|

OA

|=1，|

OB

|=k，∠AOB=

2

3

π，点C在∠AOB内，

OC

•

OA

=0，若

OC

=2m

OA

+m

OB

(m≠0)，则k=

 

．

Answer 1

分析：由点C在∠AOB=

2π

3

内，

OC

•

OA

=0，可建立如图所示的坐标系．取A（1，0），由|

OB

|=k，
可得B(kcos

2π

3

，ksin

2π

3

)，再利用

OC

=2m

OA

+m

OB

(m≠0)，可得点C的坐标，利用

OC

•

OA

=0，即可解得k．

解答：解：由点C在∠AOB=

2π

3

内，

OC

•

OA

=0，可建立如图所示的坐标系．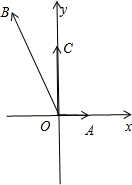
取A（1，0），
∵|

OB

|=k，∴B(kcos

2π

3

，ksin

2π

3

)，即B(-

1

2

k，

3

2

k)．
∴

OC

=2m

OA

+m

OB

(m≠0)，
∴

OC

=2m(1，0)+m(-

1

2

k，

3

2

k)=(2m-

1

2

mk，

3

2

mk)．
∵

OC

•

OA

=0，
∴2m-

1

2

mk=0，
∵m≠0，∴2-

1

2

k=0，解得k=4．
故答案为：4．

点评：本题考查了通过建立直角坐标系解决向量问题、向量的运算法则、向量的数量积与垂直的关系，属于中档题．