题目内容
(10分)已知圆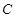 :
: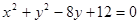 ,和定点
,和定点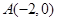 ,
,
求:(1) 过点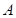 作圆
作圆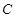 的切线
的切线 ,求直线
,求直线 方程;
方程;
(2) 过点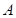 作直线
作直线 与圆
与圆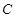 相交于
相交于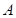 、
、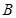 两点,且
两点,且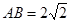 时,求直线
时,求直线 的方程.
的方程.
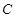 :
: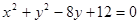 ,和定点
,和定点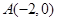 ,
,求:(1) 过点
 作圆
作圆 的切线
的切线 ,求直线
,求直线 方程;
方程;(2) 过点
 作直线
作直线 与圆
与圆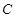 相交于
相交于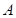 、
、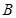 两点,且
两点,且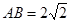 时,求直线
时,求直线 的方程.
的方程.(1) x=-2和3x-4y+6="0" (2) y=7x+14和y="x+2" 。
本试题主要是考查了线圆相切的问题,求解直线的方程的运用。以及直线与圆相交的弦长公式的运用。
(1)因为将圆C的方程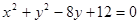 配方得标准方程为
配方得标准方程为 ,
,
则此圆的圆心为(0 , 4),半径为2.根据圆心到直线的距离可知斜率的值。注意对k的讨论是否存在的运用。
(2)若直线 的斜率不存在不合题意;设直线
的斜率不存在不合题意;设直线 的方程为y=k(x+2),
的方程为y=k(x+2),
过圆心C作CD⊥AB,则根据题意和圆的性质,关于k的关系式得到求解。
解:将圆C的方程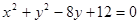 配方得标准方程为
配方得标准方程为 ,
,
则此圆的圆心为(0 , 4),半径为2.
(1)若直线 的斜率不存在时,容易验证直线x=-2,为切线;
的斜率不存在时,容易验证直线x=-2,为切线;
若直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为y=k(x+2), 与圆C相切,则有
的方程为y=k(x+2), 与圆C相切,则有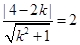 .
.
解得 ,直线
,直线 的方程为y=
的方程为y= (x+2),即3x-4y+6="0"
(x+2),即3x-4y+6="0"
综上所求直线 方程为x=-2和3x-4y+6="0"
方程为x=-2和3x-4y+6="0"
(2)若直线 的斜率不存在不合题意;设直线
的斜率不存在不合题意;设直线 的方程为y=k(x+2),
的方程为y=k(x+2),
过圆心C作CD⊥AB,则根据题意和圆的性质,得

解得 ,从而得所求直线方程为y=7x+14和y="x+2"
,从而得所求直线方程为y=7x+14和y="x+2"
(1)因为将圆C的方程
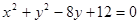 配方得标准方程为
配方得标准方程为 ,
,则此圆的圆心为(0 , 4),半径为2.根据圆心到直线的距离可知斜率的值。注意对k的讨论是否存在的运用。
(2)若直线
 的斜率不存在不合题意;设直线
的斜率不存在不合题意;设直线 的方程为y=k(x+2),
的方程为y=k(x+2),过圆心C作CD⊥AB,则根据题意和圆的性质,关于k的关系式得到求解。
解:将圆C的方程
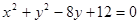 配方得标准方程为
配方得标准方程为 ,
,则此圆的圆心为(0 , 4),半径为2.
(1)若直线
 的斜率不存在时,容易验证直线x=-2,为切线;
的斜率不存在时,容易验证直线x=-2,为切线; 若直线
 的斜率存在时,设直线
的斜率存在时,设直线 的方程为y=k(x+2), 与圆C相切,则有
的方程为y=k(x+2), 与圆C相切,则有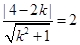 .
. 解得
 ,直线
,直线 的方程为y=
的方程为y= (x+2),即3x-4y+6="0"
(x+2),即3x-4y+6="0" 综上所求直线
 方程为x=-2和3x-4y+6="0"
方程为x=-2和3x-4y+6="0" (2)若直线
 的斜率不存在不合题意;设直线
的斜率不存在不合题意;设直线 的方程为y=k(x+2),
的方程为y=k(x+2),过圆心C作CD⊥AB,则根据题意和圆的性质,得

解得
 ,从而得所求直线方程为y=7x+14和y="x+2"
,从而得所求直线方程为y=7x+14和y="x+2" 
练习册系列答案
相关题目
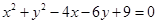 及直
及直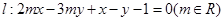
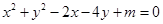 .
.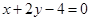 相交于M、N两点,且OM⊥ON(O为坐标原点),求m;
相交于M、N两点,且OM⊥ON(O为坐标原点),求m;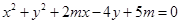 表示一个圆,
表示一个圆, 的取值范围;
的取值范围;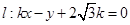 相交,求直线
相交,求直线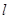 的倾斜角的取值范围.
的倾斜角的取值范围. 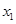 、
、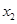 是关于x的方程
是关于x的方程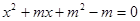 的两个不相等的实数根,那么过两点
的两个不相等的实数根,那么过两点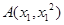 ,
,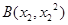 的直线与圆
的直线与圆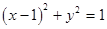 的位置关系是( )
的位置关系是( ) 截圆
截圆 得劣弧所对的圆心角弧度数为( )
得劣弧所对的圆心角弧度数为( )



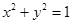 上的点到直线
上的点到直线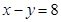 的距离的最小值
的距离的最小值 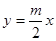 与圆
与圆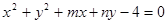 交于
交于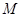 、
、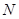 两点,且
两点,且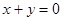 对称,则弦
对称,则弦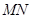 的长为( )
的长为( ) 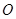 :
: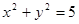 和点
和点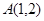 ,则过
,则过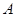 且与圆
且与圆