题目内容
甲、乙两人轮流投篮,每人每次投一票.约定甲先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束,设甲每次投篮投中的概率为 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为 ,且各次投篮互不影响。
,且各次投篮互不影响。
(1) 求甲获胜的概率;
(2) 求投篮结束时甲的投篮次数ξ的分布列与期望。
 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为 ,且各次投篮互不影响。
,且各次投篮互不影响。(1) 求甲获胜的概率;
(2) 求投篮结束时甲的投篮次数ξ的分布列与期望。
解:设Ak,Bk分别表示甲、乙在第k次投篮投中,
则P(Ak)= ,P(Bk)=
,P(Bk)= (k=1,2,3)
(k=1,2,3)
(1) 记“甲获胜”为事件C,则P(C)=P(A1)+P( )+P(
)+P( )=
)= +
+ =
= ;
;
(2) 投篮结束时甲的投篮次数?的可能值为1,2,3
P(ξ=1)=P(A1)+P( )=
)=
P(ξ=2)=P( )+P(
)+P( )=
)= =
=
P(ξ=3)=P( )=
)= =
=
∴ξ的分布列为:

期望Eξ=1× +2×
+2× +3×
+3× =
= 。
。
则P(Ak)=
 ,P(Bk)=
,P(Bk)= (k=1,2,3)
(k=1,2,3)(1) 记“甲获胜”为事件C,则P(C)=P(A1)+P(
 )+P(
)+P( )=
)= +
+ =
= ;
;(2) 投篮结束时甲的投篮次数?的可能值为1,2,3
P(ξ=1)=P(A1)+P(
 )=
)=
P(ξ=2)=P(
 )+P(
)+P( )=
)= =
=
P(ξ=3)=P(
 )=
)= =
=
∴ξ的分布列为:

期望Eξ=1×
 +2×
+2× +3×
+3× =
= 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
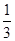 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为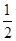 ,且各次投篮互不影响.[来(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数
,且各次投篮互不影响.[来(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数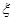 的分布列与期望
的分布列与期望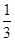 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为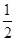 ,且各次投篮互不影响。(Ⅰ)求乙获胜的概率;(Ⅱ)求投篮结束时乙只投了2个球的概率。
,且各次投篮互不影响。(Ⅰ)求乙获胜的概率;(Ⅱ)求投篮结束时乙只投了2个球的概率。