题目内容
甲、乙两人轮流投篮直至某人投中为止,已知甲投篮每次投中的概率为0.4,乙每次投篮投中的概率为0.6,各次投篮互不影响.设甲投篮的次数为![]() ,若乙先投,且两人投篮次数之和不超过4次,求
,若乙先投,且两人投篮次数之和不超过4次,求![]() 的概率分布.
的概率分布.
![]() 的概率分布为
的概率分布为
|
| 0 | 1 | 2 |
| P | 0.6 | 0.304 | 0.096 |
解析:
因为乙先投,且次数之和不超过4次,所以,甲投篮次数的随机变量![]() 可以是0,1,2三个.
可以是0,1,2三个.
由于乙先投,若乙第一次就投中,则甲就不再投,
∴P(![]() =0)=0.6.
=0)=0.6.
当![]() =1时,它包含两种情况.
=1时,它包含两种情况.
第一种:甲第1次投中,这种情况的概率为
P1=0.4×0.4=0.16.
第二种:甲第1次未投中,乙第2次投中,这种情况的概率为P2=0.4×0.6×0.6=0.144,
∴P(![]() =1)=P1+P2=0.304.
=1)=P1+P2=0.304.
当![]() =2时,投篮终止,
=2时,投篮终止,
∴P(![]() =2)=0.4×0.6×0.4=0.096.
=2)=0.4×0.6×0.4=0.096.
∴![]() 的概率分布为
的概率分布为
|
| 0 | 1 | 2 |
| P | 0.6 | 0.304 | 0.096 |

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
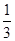 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为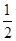 ,且各次投篮互不影响.[来(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数
,且各次投篮互不影响.[来(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数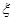 的分布列与期望
的分布列与期望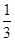 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为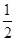 ,且各次投篮互不影响。(Ⅰ)求乙获胜的概率;(Ⅱ)求投篮结束时乙只投了2个球的概率。
,且各次投篮互不影响。(Ⅰ)求乙获胜的概率;(Ⅱ)求投篮结束时乙只投了2个球的概率。