题目内容
甲、乙两人轮流投篮，每人每次投一票.约定甲先投中者获胜，一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为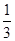
，乙每次投篮投中的概率为
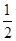，且各次投篮互不影响.[来（Ⅰ） 求甲获胜的概率；（Ⅱ）求投篮结束时甲的投篮次数
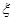的分布列与期望
【答案】
：（Ⅰ）
（Ⅱ）
【解析】：设
分别表示甲、乙在第k次投篮中，则
（Ⅰ）记“甲获胜”为事件C，由互斥事件有一个发生的概率与相互独立事件同时发生的概率计算公式知
（Ⅱ）
的所有可能值为1，2，3。
由独立性知
综上知，有分布列
|
|
|
P |
从而，
（次）
【考点定位】本题考查离散型随机变量的分布列和期望即相互独立事件的概率，考查运用概率知识解决实际问题的能力，相互独立事件是指，两事件发生的概率互不影响，注意应用相互独立事件同时发生的概率公式
练习册系列答案
优生乐园系列答案
相关题目
,若乙先投，且两人投篮次数之和不超过4次，求
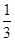，乙每次投篮投中的概率为
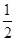，且各次投篮互不影响。（Ⅰ）求乙获胜的概率；（Ⅱ）求投篮结束时乙只投了2个球的概率。