题目内容
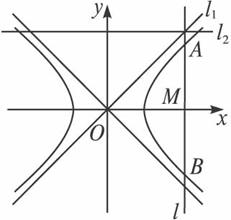
如图,直线l1:y=kx+1-k(k≠0,k≠±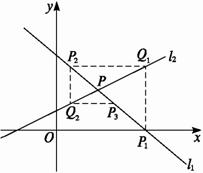
直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2……这样一直作下去,可得到一系列点P1,Q1,P2,Q2,….点Pn(n=1,2,…)的横坐标构成数列{xn}.
比较2|PPn|2与4k2|PP1|2+5的大小.
解析:由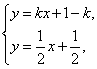 得P的坐标为(1,1).
得P的坐标为(1,1).
所以2|PPn|2=2(xn-1)2+2(kxn+1-k-1)2=8×(![]() )2n+2(
)2n+2(![]() )2n-2,?
)2n-2,?
4k2|PP1|2+5=4k2[(1-![]() -1)2+(0-1)2]+5=4k2+9.?
-1)2+(0-1)2]+5=4k2+9.?
(1)当|k|>![]() ,即k<-
,即k<-![]() 或k>
或k>![]() 时,
时,
4k2|PP1|2+5>1+9=10,?
而此时0<|![]() |<1,所以2|PPn|2<8×1+2=10.?
|<1,所以2|PPn|2<8×1+2=10.?
故2|PPn|2<4k2|PP1|2+5.?
(2)当0<|k|<![]() ,即k∈(-
,即k∈(-![]() ,0)∪(0,
,0)∪(0,![]() )时,?
)时,?
4k2|PP1|2+5<1+9=10=10,?
而此时|![]() |>1,所以2|PPn|2>8×1+2=10.?
|>1,所以2|PPn|2>8×1+2=10.?
故2|PPn|2>4k2|PP1|2+5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目