题目内容
如图,直线l:y=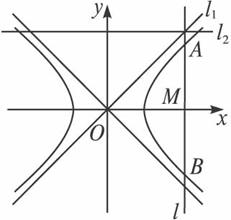
(1)求双曲线C的离心率;
(2)求双曲线C的方程.
(文)已知公差不为零的等差数列{an}的前n项和为Sn,Sn及通项an满足关系式:4Sn=an2+αan+β(α、β为常数,n∈N+),且a1=-1.
(1)求常数α、β的值;
(2)求数列{an}的通项公式.
答案:(理)解:(1)设双曲线一、三象限渐近线l1:![]() =0的倾斜角为α,
=0的倾斜角为α,
∵l和l2关于直线l1对称,记它们交点为P,而l2与x轴平行,记l2与y轴交点为Q,
依题意有∠QPO=∠POM=∠OPM=α(锐角).
又AB:y=![]() (x-2),故tan2α=
(x-2),故tan2α=![]() ,则
,则![]() ,求得tanα=
,求得tanα=![]() ,tanα=-2(舍去).
,tanα=-2(舍去).
∴![]() .因此双曲线C的离心率e=
.因此双曲线C的离心率e=![]() .
.
(2)∵![]() =
=![]() ,故设所求双曲线方程为
,故设所求双曲线方程为![]() =1,将y=
=1,将y=![]() (x-2)代入x2-4y2=4k2消去y,得
(x-2)代入x2-4y2=4k2消去y,得![]() =0.
=0.
设A(x1,y1),B(x2,y2),|AB|=![]() |x1-x2|=
|x1-x2|=![]() ·
·![]()
= .
.
化简得到![]() ,求得k2=1.故所求双曲线方程为
,求得k2=1.故所求双曲线方程为![]() -y2=1.
-y2=1.
(文)解:(1)设等差数列{an}的公差d≠0,而a1=-1,
则an=-1+(n-1)d,Sn=na1+![]() .
.
代入已知4Sn=an2+αan+β中整理得到2dn2-(4+2d)n=[nd-(d+1)]2+α[nd-(d+1)]+β.
由待定系数法,可知 由①式及d≠0求得d=2.
由①式及d≠0求得d=2.
将d=2代入②式求得α=2,再由③式求得β=-3.因此所求α=2,β=-3.
(2)由(1)求得d=2,又a1=-1,故an=a1+(n-1)d=2n-3.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A. 如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A. (2013•温州二模)如图.直线l:y=kx+1与椭圆C1:
(2013•温州二模)如图.直线l:y=kx+1与椭圆C1: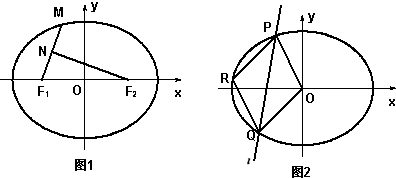
 (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=