题目内容
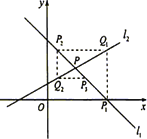
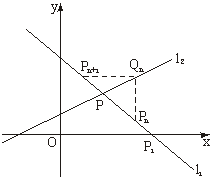
22.如图,直线l1:y=kx+1-k(k≠0,k≠±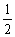
(Ⅰ)证明:xn+1-1=![]() (xn-1),n∈N*;
(xn-1),n∈N*;
(Ⅱ)求数列{xn}的通项公式;
(Ⅲ)比较2|PPn|2与4k2|PP1|2+5的大小.
22.
(Ⅰ)证明:设点Pn的坐标是(xn,yn),由已知条件得点Qn、Pn+1的坐标分别是:
(xn,![]() xn+
xn+![]() ),(xn+1,
),(xn+1, ![]() xn+
xn+![]() ).
).
由Pn+1在直线l1上,得![]() xn+
xn+![]() =kxn+1+1-k,
=kxn+1+1-k,
所以![]() (xn-1)=k(xn+1-1).
(xn-1)=k(xn+1-1).
即xn+1-1=![]() (xn-1),n∈N*.
(xn-1),n∈N*.
(Ⅱ)解:由题设知x1=1-![]() ,x1-1=-
,x1-1=-![]() ≠0,又由(Ⅰ)知xn+1-1=
≠0,又由(Ⅰ)知xn+1-1=![]() (xn-1),
(xn-1),
所以数列{xn-1}是首项为x1-1,公比为![]() 的等比数列.
的等比数列.
从而xn-1=-![]() ×(
×(![]() )n-1,即xn=1-2×(
)n-1,即xn=1-2×(![]() )n,n∈N*.
)n,n∈N*.
(Ⅲ)解:由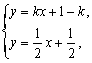 得点P的坐标为(1,1).
得点P的坐标为(1,1).
所以2|PPn|2=2(xn-1)2+2(kxn+1-k-1)2=8×(![]() )2n+2(
)2n+2(![]() )2n-2,
)2n-2,
4k2|PP1|2+5=4k2[(1-![]() -1)2+(0-1)2]+5=4k2+9.
-1)2+(0-1)2]+5=4k2+9.
(ⅰ)当|k|>![]() ,即k<-
,即k<-![]() 或k>
或k>![]() 时,4k2|PP1|2+5>1+9=10,
时,4k2|PP1|2+5>1+9=10,
而此时0<|![]() |<1,所以2|PPn|2<8×1+2=10.故2|PPn|2<4k2|PP1|2+5.
|<1,所以2|PPn|2<8×1+2=10.故2|PPn|2<4k2|PP1|2+5.
(ⅱ)当0<|k|<![]() ,即k∈(-
,即k∈(-![]() ,0)∪(0,
,0)∪(0,![]() )时,4k2|PP1|2+5<1+9=10,
)时,4k2|PP1|2+5<1+9=10,
而此时|![]() |>1,所以2|PPn|2>8×1+2=10.故2|PPn|2>4k2|PP1|2+5.
|>1,所以2|PPn|2>8×1+2=10.故2|PPn|2>4k2|PP1|2+5.

练习册系列答案
相关题目
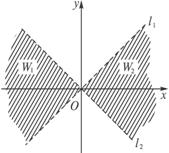
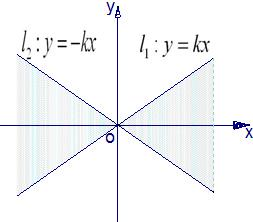 如图,直线l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
如图,直线l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.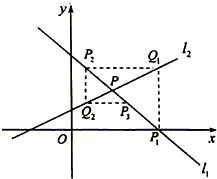 如图,直线
如图,直线