题目内容
13.已知α∈R,sinα+2cosα=$\frac{\sqrt{10}}{2}$,则tanα=( )| A. | 3 | B. | -$\frac{1}{3}$ | C. | -3 | D. | 3或-$\frac{1}{3}$ |
分析 sinα+2cosα=$\frac{\sqrt{10}}{2}$,两边平方可得:sin2α+4cos2α+4sinαcosα=$\frac{5}{2}$,把分母看做1,利用“弦化切”可得:$\frac{ta{n}^{2}α+4tanα+4}{ta{n}^{2}α+1}$=$\frac{5}{2}$,化简解出即可得出.
解答 解:∵sinα+2cosα=$\frac{\sqrt{10}}{2}$,
两边平方可得:sin2α+4cos2α+4sinαcosα=$\frac{5}{2}$,
∴$\frac{si{n}^{2}α+4co{s}^{2}α+4sinαcosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{5}{2}$,
化为$\frac{ta{n}^{2}α+4tanα+4}{ta{n}^{2}α+1}$=$\frac{5}{2}$,
化为:3tan2α-8tanα-3=0,
解得tanα=3或-$\frac{1}{3}$.
故选:D.
点评 本题考查了同角三角函数基本关系式、方程的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上一点与其左顶点、右焦点构成以右焦点为直角顶点的等腰三角形,则此双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$+\sqrt{2}$ |
2.设单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为$\frac{2π}{3}$,$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=2$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$,则$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为( )
| A. | -$\frac{3\sqrt{3}}{2}$ | B. | -$\frac{2\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
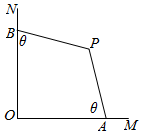 某菜农有两段总长度为20米的篱笆PA及PB,现打算用它们和两面成直角的墙OM、ON围成一个如图所示的四边形菜园OAPB(假设OM、ON这两面墙都足够长).已知|PA|=|PB|=10(米),∠AOP=∠BOP=$\frac{π}{4}$,∠OAP=∠OBP.设∠OAP=θ,四边形OAPB的面积为S.
某菜农有两段总长度为20米的篱笆PA及PB,现打算用它们和两面成直角的墙OM、ON围成一个如图所示的四边形菜园OAPB(假设OM、ON这两面墙都足够长).已知|PA|=|PB|=10(米),∠AOP=∠BOP=$\frac{π}{4}$,∠OAP=∠OBP.设∠OAP=θ,四边形OAPB的面积为S.