题目内容
4.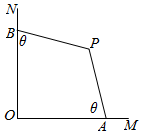 某菜农有两段总长度为20米的篱笆PA及PB,现打算用它们和两面成直角的墙OM、ON围成一个如图所示的四边形菜园OAPB(假设OM、ON这两面墙都足够长).已知|PA|=|PB|=10(米),∠AOP=∠BOP=$\frac{π}{4}$,∠OAP=∠OBP.设∠OAP=θ,四边形OAPB的面积为S.
某菜农有两段总长度为20米的篱笆PA及PB,现打算用它们和两面成直角的墙OM、ON围成一个如图所示的四边形菜园OAPB(假设OM、ON这两面墙都足够长).已知|PA|=|PB|=10(米),∠AOP=∠BOP=$\frac{π}{4}$,∠OAP=∠OBP.设∠OAP=θ,四边形OAPB的面积为S.(1)将S表示为θ的函数,并写出自变量θ的取值范围;
(2)求出S的最大值,并指出此时所对应θ的值.
分析 (1)在三角POB中,由正弦定理,得:$\frac{OB}{{sin(\frac{3π}{4}-θ)}}=\frac{10}{{sin\frac{π}{4}}}$,得OB=10(cosθ+sinθ).再利用三角形面积计算公式即可得出.
(2)由(1)利用倍角公式与和差公式、三角函数的单调性最值即可得出.
解答 解:(1)在三角POB中,由正弦定理,得:$\frac{OB}{{sin(\frac{3π}{4}-θ)}}=\frac{10}{{sin\frac{π}{4}}}$,得OB=10(cosθ+sinθ).
所以,S=$2×\frac{1}{2}×10×10(cosθ+sinθ)sinθ$=100(sinθcosθ+sin2θ),θ∈$(0,\frac{π}{4})$∪$(\frac{π}{4},\frac{3π}{4})$.
(2)S=100(sinθcosθ+sin2θ)=50(2sinθcosθ+2sin2θ)
=50(sin2θ-cos2θ+1)=$50\sqrt{2}sin(2θ-\frac{π}{4})+50$,
所以S的最大值为:50$\sqrt{2}$+50,θ=$\frac{3π}{8}$.
点评 本题考查了正弦定理、和差公式、倍角公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
14.集合A={x|-1<x<3},集合B={x|-1<x<2},则A∩B=( )
| A. | (1,2) | B. | (-1,2) | C. | (1,3) | D. | (-1,3) |
15.某校体育教研组研发了一项新的课外活动项目,为了解该项目受欢迎程度,在某班男女中各随机抽取20名学生进行调研,统计得到如下列联表:
附:参考公式及数据
(1)在喜欢这项课外活动项目的学生中任选1人,求选到男生的概率;
(2)根据题目要求,完成2×2列联表,并判断是否有95%的把握认为“喜欢该活动项目与性别有关”?
| 喜欢 | 不喜欢 | 总计 | |
| 女生 | 15 | ||
| 男生 | 12 | 20 | |
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
(2)根据题目要求,完成2×2列联表,并判断是否有95%的把握认为“喜欢该活动项目与性别有关”?
12.设函数$f(x)=\left\{{\begin{array}{l}{1+{{log}_3}(2-x),(x<1)}\\{{3^{x-1}},(x≥1)}\end{array}}\right.$,则f(-7)+f(log312)=( )
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
16.已知f(x)=$\frac{3+5×({-1)}^{x}}{2}$,则如图所示的程序框图运行之后输出的结果为( )


| A. | 3016 | B. | 3020 | C. | 3024 | D. | 3028 |
13.已知α∈R,sinα+2cosα=$\frac{\sqrt{10}}{2}$,则tanα=( )
| A. | 3 | B. | -$\frac{1}{3}$ | C. | -3 | D. | 3或-$\frac{1}{3}$ |