题目内容
若将一个标有1,2,3,4,5,6六个数字的正方体玩具抛掷五次,则其中不少于四次出现偶数的概率是 .
考点:n次独立重复试验中恰好发生k次的概率,互斥事件的概率加法公式
专题:计算题,概率与统计
分析:根据题意,分析可得抛掷1次该玩具出现偶数的概率为
,而五次抛掷中不少于4次出现偶数即出现4次偶数或5次偶数,分别求出出现4次偶数或5次偶数的概率,进而由互斥事件概率公式计算可得答案.
| 1 |
| 2 |
解答:
解:根据题意,将一个标有1,2,3,4,5,6六个数字的正方体玩具抛掷1次,
出现奇数与偶数的概率相等,均为
,
则出现4次偶数的概率为P1=
×(
)4×
=
,
出现5次偶数的概率为P2=
×(
)5=
,
故其中不少于4次出现偶数的概率P=
+
=
;
故答案为:
.
出现奇数与偶数的概率相等,均为
| 1 |
| 2 |
则出现4次偶数的概率为P1=
| C | 4 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 32 |
出现5次偶数的概率为P2=
| C | 5 5 |
| 1 |
| 2 |
| 1 |
| 32 |
故其中不少于4次出现偶数的概率P=
| 5 |
| 32 |
| 1 |
| 32 |
| 3 |
| 16 |
故答案为:
| 3 |
| 16 |
点评:本题考查互斥事件、n次独立重复试验恰有k次发生的概率,首先要分析每一次试验出现偶数的概率.

练习册系列答案
相关题目
已知函数f0(x)=xex,f1(x)=f0′(x),f2(x)=f1′(x),…fn(x)=fn-1′(x)(n∈N*)则f2014′(0)=( )
| A、2013 | B、2014 |
| C、2015 | D、2016 |
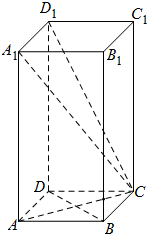 已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.
已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.