题目内容

设f(x)=
ln(x-2)，x＞2
2x+
∫
a
0
3t2dt，x≤2
，若f（f（3））=9，则a的值是（　　）
A、1B、2C、3D、4
考点：定积分,函数的值
专题：函数的性质及应用
分析：利用分段函数的性质和定积分知识求解．
解答： 解：∵f(x)=
ln(x-2)，x＞2
2x+
∫
a
0
3t2dt，x≤2
，f（f（3））=9，
∴f（3）=ln1=0，
f（f（3））=f（0）=20+[t3]
|
a
0
=9，
∴a3=8，解得a=2．
故选：B．
点评：本题考查函数值的求法及应用，是基础题，解题时要注意定积分的合理运用．
练习册系列答案
相关题目
已知数列{an}满足an+1=
1
2
an+
1
2n+1
（n≥1），其中a1=
1
4

（Ⅰ）求a1，a2，a3；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）求数列{an}的前n项和Sn．
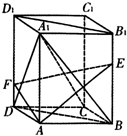如图，在长方体A BCD-A1B1C1D1中，点E，F分别在BB1，DD1上，且AE⊥A1B，AF⊥A1D．
（I）求证：A1C⊥平面AEF；
（Ⅱ）若AB=4，AD=3，AA1=5，求平面AEF和平面D1B1BD所成的角的余弦值．
已知4x=5y=10，则
1
x
+
2
y
=
 
．
已知α是第二象限角，且sin（
π
2
+α）=-
1
3
，则tan2α的值为（　　）
A、
4
2
7
B、-
4
2
7
C、
4
2
9
D、-
4
2
9
若复数z满足z=（z-1）•i，则复数z的模为（　　）
A、1
B、
2
2
C、
2
D、2
设F1、F2为椭圆
x2
4
+y2=1的左、右焦点，过椭圆中心任作一直线与椭圆交于P，Q两点，当四边形PF1QF2面积最大时，
PF1
•
PF2
的值等于
 
．
已知有穷数列{an}各项均不相等，将{an}的项从大到小重新排序后相应的项数构成新数列{pn}，称{pn}为{an}的“序数列”．例如数列：a1，a2，a3满足a1＞a3＞a2，则其序数列{pn}为1，3，2．
（1）若x，y∈R+，x+y=2且x≠y，写出数列：1，xy，
x2+y2
2
的序数列并说明理由；
（2）求证：有穷数列{an}的序数列{pn}为等差数列的充要条件是有穷数列{an}为单调数列；
（3）若项数不少于5项的有穷数列{bn}、{cn}的通项公式分别是bn=n•(
3
5
)n（n∈N*），cn=-n2+tn（n∈N*），且{bn}的序数列与{cn}的序数列相同，求实数t的取值范围．
数列{an}满足an=2an-1+2n+1（n∈N*，n≥2），a1=2．
（1）设bn=
1
2n
（an+1），求证：数列{bn}是等差数列；
（2）求数列{an}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网