题目内容
设三角形ABC的内角A,B,C的对边分别为a,b,c,且acosC=b-
c.
(Ⅰ)求角A的大小;
(Ⅱ)若a=
,求三角形ABC面积S的最大值.
| 1 |
| 2 |
(Ⅰ)求角A的大小;
(Ⅱ)若a=
| 3 |
考点:正弦定理,余弦定理
专题:解三角形
分析:(Ⅰ)利用正弦定理化简已知等式,根据sinB=sin(A+C),利用两角和与差的正弦函数公式化简,整理后求出cosA的值,即可确定出角A的大小;
(Ⅱ)利用余弦定理列出关系式,将a,cosA的值代入得到关系式,利用基本不等式求出bc的最大值,即可确定出三角形ABC面积S的最大值.
(Ⅱ)利用余弦定理列出关系式,将a,cosA的值代入得到关系式,利用基本不等式求出bc的最大值,即可确定出三角形ABC面积S的最大值.
解答:
解:(Ⅰ)由正弦定理化简acosC=b-
c得:sinAcosC=sinB-
sinC,
即sinAcosC=sin(A+C)-
sinC=sinAcosC+cosAsinC-
sinC,
∴cosAsinC-
sinC=0,
又sinC≠0,
∴cosA=
,
∵0<A<π,
∴A=
;
(Ⅱ)∵a=
,cosA=
,
∴由余弦定理得cosA=
=
,即b2+c2=bc+3,
∵b2+c2≥2bc,当且仅当b=c时取等号,
∴bc+3≥2bc,即bc≤3,
∴S△ABC=
bcsinA≤
×3×
=
,
则当b=c=
时,三角形ABC面积S的最大值为
.
| 1 |
| 2 |
| 1 |
| 2 |
即sinAcosC=sin(A+C)-
| 1 |
| 2 |
| 1 |
| 2 |
∴cosAsinC-
| 1 |
| 2 |
又sinC≠0,
∴cosA=
| 1 |
| 2 |
∵0<A<π,
∴A=
| π |
| 3 |
(Ⅱ)∵a=
| 3 |
| 1 |
| 2 |
∴由余弦定理得cosA=
| b2+c2-3 |
| 2bc |
| 1 |
| 2 |
∵b2+c2≥2bc,当且仅当b=c时取等号,
∴bc+3≥2bc,即bc≤3,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
则当b=c=
| 3 |
3
| ||
| 4 |
点评:此题考查了正弦、余弦定理,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
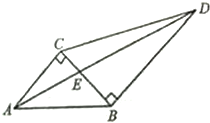 如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.
如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.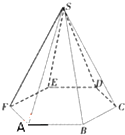 正六棱锥的底面周长为24,侧面与底面所成角为60°.求:
正六棱锥的底面周长为24,侧面与底面所成角为60°.求: