题目内容
已知抛物线y2=2px(p>0)的焦点为F,过点F且倾斜角为60°的直线与抛物线交于A,B两点.若|AF|=4,则|BF|= .
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设抛物线y2=2px(p>0)的准线为l.如图所示,分别过点A,B作AM⊥l,BN⊥l,垂足为M,N.过点B作BC⊥AM交于点C.由抛物线的定义可得:|AM|=|AF|,|BN|=|BF|.由于AM∥x轴,∠BAC=∠AFx=60°.在Rt△ABC中,|AC|=
|AB|.化简即可得出.
| 1 |
| 2 |
解答:
解:设抛物线y2=2px(p>0)的准线为l:x=-
.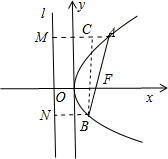
如图所示,分别过点A,B作AM⊥l,BN⊥l,垂足为M,N.
过点B作BC⊥AM交于点C.
则|AM|=|AF|,|BN|=|BF|.
∵AM∥x轴,
∴∠BAC=∠AFx=60°.
在Rt△ABC中,|AC|=
|AB|
又|AM|-|BN|=|AC|,
∴|AF|-|BF|=
(|AF|+|BF|),
化为|AF|=3|BF|
∵|AF|=4,
∴|BF|=
或12.
故答案为:
或12.
| p |
| 2 |

如图所示,分别过点A,B作AM⊥l,BN⊥l,垂足为M,N.
过点B作BC⊥AM交于点C.
则|AM|=|AF|,|BN|=|BF|.
∵AM∥x轴,
∴∠BAC=∠AFx=60°.
在Rt△ABC中,|AC|=
| 1 |
| 2 |
又|AM|-|BN|=|AC|,
∴|AF|-|BF|=
| 1 |
| 2 |
化为|AF|=3|BF|
∵|AF|=4,
∴|BF|=
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题考查了抛物线的定义、含60°角的直角三角形的性质、平行线的性质,考查了辅助线的作法,属于中档题.

练习册系列答案
相关题目