题目内容
8.关于函数$y=2sin(3x+\frac{π}{4})+1$,下列叙述有误的是( )| A. | 其图象关于直线$x=-\frac{π}{4}$对称 | |
| B. | 其图象可由$y=2sin(x+\frac{π}{4})+1$图象上所有点的横坐标变为原来的$\frac{1}{3}$倍得到 | |
| C. | 其图象关于点$(\frac{11π}{12},0)$对称 | |
| D. | 其值域是[-1,3] |
分析 利用正弦函数的图象和性质,判断各个选项是否正确,从而得出结论.
解答 解:关于函数$y=2sin(3x+\frac{π}{4})+1$,令x=-$\frac{π}{4}$,求得y=-1,为函数的最小值,故A正确;
由$y=2sin(x+\frac{π}{4})+1$图象上所有点的横坐标变为原来的$\frac{1}{3}$倍,可得y=2sin(3x+$\frac{π}{4}$)的图象,故B正确;
令x=$\frac{11π}{12}$,求得y=1,可得函数的图象关于点($\frac{11π}{12}$,1)对称,故C错误;
函数的值域为[-1,3],故D正确,
故选:C.
点评 本题主要考查正弦函数的图象和性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知集合M={x|0<x<3},N={x|x>2},则M∩(∁RN)=( )
| A. | (0,2] | B. | [0,2) | C. | (2,3) | D. | [2,3) |
3.下列函数中,既是奇函数又在(0,+∞)单调递增的函数是( )
| A. | y=ex+e-x | B. | y=ln(|x|+1) | C. | $y=\frac{sinx}{|x|}$ | D. | $y=x-\frac{1}{x}$ |
13.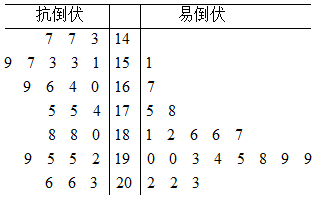 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
(1)完成2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
(2)(i)按照分层抽样的方式,在上述样本中,从易倒伏和抗倒伏两组中抽出9株玉米,设取出的易倒伏矮茎玉米株数为X,求X的分布列(概率用组合数算式表示)
(ii)若将频率视为概率,从抗倒伏的玉米试验田中再随机取出50株,求取出的高茎玉米株数的数学期望和方差
( ${{K}^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.(1)完成2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
(2)(i)按照分层抽样的方式,在上述样本中,从易倒伏和抗倒伏两组中抽出9株玉米,设取出的易倒伏矮茎玉米株数为X,求X的分布列(概率用组合数算式表示)
(ii)若将频率视为概率,从抗倒伏的玉米试验田中再随机取出50株,求取出的高茎玉米株数的数学期望和方差
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20.如图是民航部门统计的2017年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图表,根据图表,下面叙述不正确的是( )

| A. | 深圳的变化幅度最小,北京的平均价格最高 | |
| B. | 深圳和厦门的春运期间往返机票价格同去年相比有所下降 | |
| C. | 平均价格从高到低居于前三位的城市为北京、深圳、广州 | |
| D. | 平均价格变化量从高到低居于前三位的城市为天津、西安、厦门 |

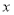 ,
,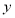 满足约束条件
满足约束条件 若
若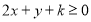 恒成立,则实数
恒成立,则实数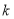 的取值范围为 .
的取值范围为 .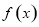 是定义在
是定义在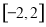 上的奇函数,当
上的奇函数,当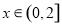 时,
时,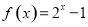 ,函数
,函数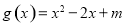 ,如果对于
,如果对于 ,使得
,使得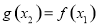 ,则实数
,则实数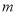 的取值范围是__________.
的取值范围是__________.