题目内容
3．下列函数中，既是奇函数又在（0，+∞）单调递增的函数是（ ）| A． | y=ex+e-x | B． | y=ln（|x|+1） | C． | $y=\frac{sinx}{|x|}$ | D． | $y=x-\frac{1}{x}$ |
分析 根据函数的单调性和奇偶性判断即可．
解答 解：对于A、B选项为偶函数，排除，
C选项是奇函数，但在（0，+∞）上不是单调递增函数．
故选：D．
点评 本题考查函数的单调性与奇偶性知识．
练习册系列答案
相关题目
16．已知集合U={1，2，3，4，5，6}M={1，2}，N={2，3，4}，则M∩（∁UN）=（ ）
| A． | {1} | B． | {2} | C． | {1，2，5，6} | D． | {1，2，3，4} |
17．设f′（x）、g′（x）分别是函数f（x）、g（x）（x∈R）的导数，且满足g（x）＞0，f′（x）g（x）-f（x）g′（x）＞0．若△ABC中，∠C是钝角，则（ ）
| A． | f（sinA）•g（sinB）＞f（sinB）•g（sinA） | B． | f（sinA）•g（sinB）＜f（sinB）•g（sinA） | ||
| C． | f（cosA）•g（sinB）＞f（sinB）•g（cosA） | D． | f（cosA）•g（sinB）＜f（sinB）•g（cosA） |
8．关于函数$y=2sin（3x+\frac{π}{4}）+1$，下列叙述有误的是（ ）
| A． | 其图象关于直线$x=-\frac{π}{4}$对称 | |
| B． | 其图象可由$y=2sin（x+\frac{π}{4}）+1$图象上所有点的横坐标变为原来的$\frac{1}{3}$倍得到 | |
| C． | 其图象关于点$（\frac{11π}{12}，0）$对称 | |
| D． | 其值域是[-1，3] |
11．已知圆C：（x-1）2+y2=r2（r＞0）．设条件p：0＜r＜3，条件q：圆C上至多有2个点到直线x-$\sqrt{3}$y+3=0的距离为1，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
．
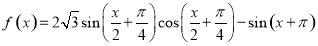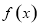的最小正周期；
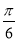个单位，得到函数
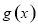的图象，求函数
在区间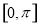
上的最大值和最小值．