题目内容
8.已知函数f(x)=|x+$\frac{2{a}^{2}+1}{a}$|+|x-a|(a>0)(Ⅰ)证明:f(x)≥2$\sqrt{3}$;
(Ⅱ)当a=1时,求不等式f(x)≥5的解集.
分析 (Ⅰ)根据绝对值的性质以及基本不等式的性质证明即可;(Ⅱ)将a的值代入,通过讨论x的范围求出不等式的解集即可.
解答 解:(Ⅰ)∵a>0,
∴f(x)=|x+$\frac{2{a}^{2}+1}{a}$|+|x-a|≥|x+2a+$\frac{1}{a}$-x+a|=3a+$\frac{1}{a}$≥2$\sqrt{3a•\frac{1}{a}}$=2$\sqrt{3}$,
当且仅当3a=$\frac{1}{a}$即a=$\frac{\sqrt{3}}{3}$时”=“成立;
(Ⅱ)a=1时,f(x)=|x+3|+|x-1|≥5,
x≥1时,x+3+x-1≥5,解得:x≥$\frac{3}{2}$,
-3<x<1时,x+3+1-x=4≥5,无解,
x≤-3时,-x-3-x+1=-2x-2≥5,解得:x≤-$\frac{7}{2}$,
故不等式的解集是{x|x≥$\frac{3}{2}$或x≤-$\frac{7}{2}$}.
点评 本题考查了解绝对值不等式问题,考查基本不等式的性质,是一道中档题.

练习册系列答案
相关题目

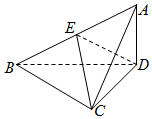 已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.