题目内容
19.已知向量$\overrightarrow{p}$=(1,2),$\overrightarrow{q}$=(x,3),若$\overrightarrow{p}$⊥$\overrightarrow{q}$,则|$\overrightarrow{p}$+$\overrightarrow{q}$|=5$\sqrt{2}$.分析 $\overrightarrow{p}$⊥$\overrightarrow{q}$,可得$\overrightarrow{p}•\overrightarrow{q}$=0,解得x.再利用向量模的计算公式即可得出.
解答 解:∵$\overrightarrow{p}$⊥$\overrightarrow{q}$,∴$\overrightarrow{p}•\overrightarrow{q}$=x+6=0,解得x=-6.
∴$\overrightarrow{p}+\overrightarrow{q}$=(-5,5).
∴|$\overrightarrow{p}$+$\overrightarrow{q}$|=$\sqrt{(-5)^{2}+{5}^{2}}$=5$\sqrt{2}$.
故答案为:5$\sqrt{2}$.
点评 本题考查了向量垂直与数量积的关系、向量模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10.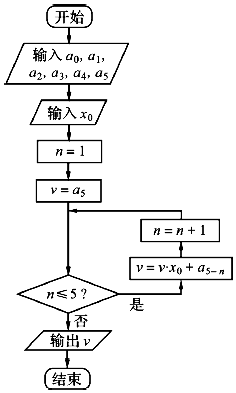 执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )
执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )
 执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )
执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )| A. | 15 | B. | 3 | C. | -3 | D. | -15 |
14.已知函数f(x)的图象与函数y=x3-3x2+2的图象关于点($\frac{1}{2}$,0)对称,过点(1,t)仅能作曲线y=f(x)的一条切线,则实数t的取值范围是( )
| A. | (-3,-2) | B. | [-3,-2] | C. | (-∞,-3)∪(-2,+∞) | D. | (-∞,-3)∪[-2,+∞) |
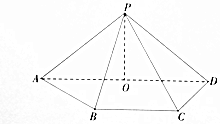 如图,四棱锥P-ABCD中,O为AD的中点,AD∥BC,CD⊥平面PAD,PA=PD=5.
如图,四棱锥P-ABCD中,O为AD的中点,AD∥BC,CD⊥平面PAD,PA=PD=5. 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈R,λ>0),
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈R,λ>0),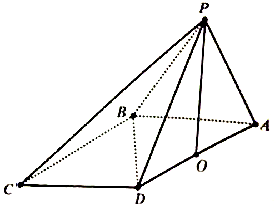 在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.
在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.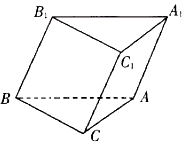 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2.