题目内容
已知圆O:x2+y2=4和点M(1,a),
(1)若过点M有且只有一条直线与圆O相切,求实数a的值,并求出切线方程;
(2)若a=2,圆O上有一动点N(x0,y0),设线段MN上一点P满足MP=2PN,求点P的轨迹方程.
(1)若过点M有且只有一条直线与圆O相切,求实数a的值,并求出切线方程;
(2)若a=2,圆O上有一动点N(x0,y0),设线段MN上一点P满足MP=2PN,求点P的轨迹方程.
考点:轨迹方程,圆的切线方程
专题:直线与圆
分析:(1)由条件知点M在圆O上,从而a=±
,由此能求出切线方程.
(2)由MP=2PN,设P(x,y),M(1,2),N(x0,y0),则(x-1,y-2)=2(x0-x,y0-y),由此得
,再由动点N(x0,y0)在圆上,能求出点P的轨迹方程.
| 3 |
(2)由MP=2PN,设P(x,y),M(1,2),N(x0,y0),则(x-1,y-2)=2(x0-x,y0-y),由此得
|
解答:
解:(1)由条件知点M在圆O上,
所以,1+a2=4,即a=±
,
当a=
时,点M为(1,
),kOM=
,k切线=-
,
此时,切线方程为y-
=-
(x-1),
即x+
y-4=0.
当a=-
时,点M为(1,-
),
=-
,k切线=
,
此时,切线方程为y+
=
(x-1),
即x-
y-4=0.
所以,所求的切线方程为x+
y-4=0或x-
y-4=0.
(2)由MP=2PN,设P(x,y),M(1,2),N(x0,y0),
则(x-1,y-2)=2(x0-x,y0-y),
∴
,解得
,
∵动点N(x0,y0)在圆上,
∴
+
=4,
即(3x-1)2+(3y-2)2=16,
∴点P的轨迹方程为(3x-1)2+(3y-2)2=16.
所以,1+a2=4,即a=±
| 3 |
当a=
| 3 |
| 3 |
| 3 |
| ||
| 3 |
此时,切线方程为y-
| 3 |
| ||
| 3 |
即x+
| 3 |
当a=-
| 3 |
| 3 |
| k | OM |
| 3 |
| ||
| 3 |
此时,切线方程为y+
| 3 |
| ||
| 3 |
即x-
| 3 |
所以,所求的切线方程为x+
| 3 |
| 3 |
(2)由MP=2PN,设P(x,y),M(1,2),N(x0,y0),
则(x-1,y-2)=2(x0-x,y0-y),
∴
|
|
∵动点N(x0,y0)在圆上,
∴
| (3x-1)2 |
| 4 |
| (3y-2)2 |
| 4 |
即(3x-1)2+(3y-2)2=16,
∴点P的轨迹方程为(3x-1)2+(3y-2)2=16.
点评:本题考查圆的切线方程和点的轨迹方程的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
相关题目
已知m,n是两条不同直线,α,β是两个不同的平面,且n?β,则下列叙述正确的是( )
| A、若m∥n,m?α,则α∥β |
| B、若α∥β,m?α,则m∥n |
| C、若m∥n,m⊥α,则α⊥β |
| D、若α∥β,m⊥n,则m⊥α |
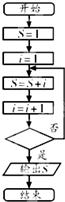 阅读如图所示的程序框图( 框图中的赋值符号“=”也可以写成“←”或“:=”),若输出S的值等于7,那么在程序框图中的判断框内应填写的条件是( )
阅读如图所示的程序框图( 框图中的赋值符号“=”也可以写成“←”或“:=”),若输出S的值等于7,那么在程序框图中的判断框内应填写的条件是( )| A、i>2? | B、i>3? |
| C、i>4? | D、i>5? |
已知直线x-2y-a=0与圆:x2+y2+2x-4y=0相切,则a=( )
| A、0 | B、-10或0 |
| C、-3或0 | D、--10 |
已知抛物线C:y2=8x,过点P(2,0)的直线与抛物线交于A,B两点,O为坐标原点,则
•
的值为( )
| OA |
| OB |
| A、-16 | B、-12 | C、4 | D、0 |