题目内容
17.从点P(2,-1)向圆x2+y2-2mx-2y+m2=0作切线,当切线长最短时m的值为( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 确定圆心与半径,利用切线长最短时,CP最小,可得结论.
解答 解:圆x2+y2-2mx-2y+m2=0,可化为圆(x-m)2+(y-1)2=1,圆心C(m,1),半径为1,
切线长最短时,CP最小,|CP|=$\sqrt{(m-2)^{2}+4}$,
∴m=2时,CP最小,切线长最短.
故选:D.
点评 本题考查圆的切线,考查学生的计算能力,利用切线长最短时,CP最小是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.抛物线的准线方程是y=-1,则抛物线的标准方程是( )
| A. | x2=4y | B. | x2=-4y | C. | y2=4x | D. | y2=-4x |
9.下列函数中,是奇函数且在(0,1]上单调递减的函数是( )
| A. | y=-x2+2x | B. | y=x+$\frac{1}{x}$ | C. | y=2x-2-x | D. | y=1-$\sqrt{x}$ |
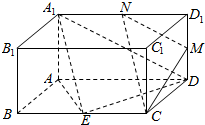 如图,长方体ABCD-A1B1C1D1中,AA1=AB=1,AD=2,E为BC的中点,点M,N分别为棱DD1,A1D1的中点.
如图,长方体ABCD-A1B1C1D1中,AA1=AB=1,AD=2,E为BC的中点,点M,N分别为棱DD1,A1D1的中点.