题目内容
5. 如图,在四面体P-ABC中,PA=PB=PC=4,点O是点P在平面ABC上的投影,且tan∠APO=$\frac{\sqrt{2}}{2}$,则四面体P-ABC的外接球的体积为( )
如图,在四面体P-ABC中,PA=PB=PC=4,点O是点P在平面ABC上的投影,且tan∠APO=$\frac{\sqrt{2}}{2}$,则四面体P-ABC的外接球的体积为( )| A. | 8$\sqrt{6}$π | B. | 24π | C. | 32$\sqrt{3}$π | D. | 48π |
分析 推导出AO=$\frac{4\sqrt{3}}{3}$,PO=$\frac{4\sqrt{6}}{3}$,由题意知四面体P-ABC的外接球的球心O′在线段PO上,从而O′O2+AO2=AO'2,进而求得R=$\sqrt{6}$,由此能求出四面体P-ABC的外接球的体积.
解答 解:∵在四面体P-ABC中,PA=PB=PC=4,点O是点P在平面ABC上的投影,且tan∠APO=$\frac{\sqrt{2}}{2}$,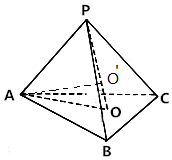
∴sin∠APO=$\frac{\sqrt{3}}{3}$,cos$∠APO=\frac{\sqrt{6}}{3}$,
∴AO=$\frac{4\sqrt{3}}{3}$,PO=$\frac{4\sqrt{6}}{3}$,
由题意知四面体P-ABC的外接球的球心O′在线段PO上,
∴O′O2+AO2=AO'2,
∴($\frac{4\sqrt{6}}{3}-R$)2+($\frac{4\sqrt{3}}{3}$)2=R2,解得R=$\sqrt{6}$,
∴四面体P-ABC的外接球的体积为8$\sqrt{6}$π.
故选:A.
点评 本题考查四面体的外接球的体积的求法,是中档题,解题时要认真审题,注意四面体、球的性质的合理运用.

练习册系列答案
相关题目
20.已知有线性相关关系的两个变量建立的回归直线方程为$\stackrel{∧}{y}$=$\stackrel{∧}{a}$+$\stackrel{∧}{b}$x,方程中的回归系数$\stackrel{∧}{b}$( )
| A. | 可以小于0 | B. | 只能大于0 | C. | 可以为0 | D. | 只能小于0 |
1.若经过点A(3,a)、B(4,-4)的直线与经过点C(-2,0)且斜率为2的直线垂直,则a的值为( )
| A. | -$\frac{7}{2}$ | B. | $\frac{15}{4}$ | C. | 10 | D. | -10 |