题目内容
3.近年来空气污染是一个生活中重要的话题,PM2.5就是其中一个重要指标.各省、市、县均要进行实时监测,某市2015年11月的PM2.5浓度统计如图所示.| 日期 | PM2.5浓度 | 日期 | PM2.5浓度 | 日期 | PM2.5浓度 |
| 11-1 | 137 | 11-11 | 144 | 11-21 | 40 |
| 11-2 | 143 | 11-12 | 166 | 11-22 | 42 |
| 11-3 | 145 | 11-13 | 197 | 11-23 | 35 |
| 11-4 | 193 | 11-14 | 194 | 11-24 | 53 |
| 11-5 | 133 | 11-15 | 219 | 11-25 | 88 |
| 11-6 | 22 | 11-16 | 41 | 11-26 | 29 |
| 11-7 | 22 | 11-17 | 90 | 11-27 | 199 |
| 11-8 | 57 | 11-18 | 46 | 11-28 | 287 |
| 11-9 | 111 | 11-19 | 80 | 11-29 | 291 |
| 11-10 | 134 | 11-20 | 67 | 11-30 | 452 |
| 空气质量指数类别 | PM2.5 24小时浓度均值 | 频数 | 频率 |
| 优 | 0-35 | 4 | $\frac{2}{15}$ |
| 良 | 36-75 | 7 | $\frac{7}{30}$ |
| 轻度污染 | 76-115 | 4 | |
| 中度污染 | 116-150 | 6 | |
| 重度污染 | 151-250 | ||
| 严重污染 | 251-500 | ||
| 合计 | / | 30 | 1 |
(3)PM2.5浓度在75以上,空气质量为超标,陶先生在2015年11月份期间曾有两天经过该市,记ξ表示两天中PM2.5检测数据超标的天数,求ξ的分布列及期望.
分析 (Ⅰ)由已知条件能求出频率分布表.
(Ⅱ) 学校进行了连续两天的户外拔河比赛,要能正常进行,利用列举法求出需选择的日期,由此能求出拔河比赛能正常进行的概率.
(Ⅲ)ξ的可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列及期望.
解答 解:(Ⅰ)由已知条件能求出频率分布表:
| 空气质量指数类别 | PM2.5 24小时浓度均值 | 频数 | 频率 |
| 优 | 0-35 | 4 | $\frac{2}{15}$ |
| 良 | 36-75 | 7 | $\frac{7}{30}$ |
| 轻度污染 | 76-115 | 4 | $\frac{2}{15}$ |
| 中度污染 | 116-150 | 6 | $\frac{1}{5}$ |
| 重度污染 | 151-250 | 6 | $\frac{1}{5}$ |
| 严重污染 | 251-500 | 3 | $\frac{1}{10}$ |
| 合计 | 30 | 1 |
(Ⅱ) 学校进行了连续两天的户外拔河比赛,要能正常进行,需选择的日期为:
(6,7)(7,8)(8,9)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)(23,24)(24,25)(25,26),
所以拔河比赛能正常进行的概率为$\frac{13}{29}$. …(6分)
(Ⅲ)ξ的可能取值为0,1,2,
$P(ξ=0)=\frac{{C_{11}^2}}{{C_{30}^2}}=\frac{11}{87}$,
$P(ξ=1)=\frac{{C_{11}^1C_{19}^1}}{{C_{30}^2}}=\frac{209}{435}$,
$P(ξ=2)=\frac{{C_{19}^2}}{{C_{30}^2}}=\frac{57}{145}$…(9分)
∴ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{11}{87}$ | $\frac{209}{435}$ | $\frac{57}{145}$ |
$Eξ=\frac{11}{87}×0+\frac{209}{435}×1+\frac{57}{145}×2=\frac{551}{435}=\frac{19}{15}$…(12分)
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
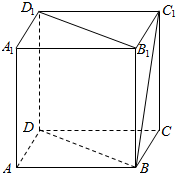 如图,正方体ABCD-A1B1C1D1中,直线BC1和B1D1所成角的大小为60°;直线BC1和平面B1D1DB所成角的大小为30°.
如图,正方体ABCD-A1B1C1D1中,直线BC1和B1D1所成角的大小为60°;直线BC1和平面B1D1DB所成角的大小为30°.