题目内容
12．在数列{an}中，a1=2，an+1=an+2n（n∈N*），则数列{an}的通项公式为2n．分析 利用累加法以及等比数列求和求解即可．
解答 解：在数列{an}中，a1=2，an+1=an+2n（n∈N*），
a1=2，
a2=a1+21
a3=a2+22
a4=a3+23
…
an=an-1+2n-1
累加可得：an=2+2+22+23+…+2n-1
=$\frac{2（1-{2}^{n-1}）}{1-2}$+2=2n．
则数列{an}的通项公式为：2n．
故答案为：2n．
点评 本题考查数列递推关系式的应用，累加法的应用以及等比数列求和，考查计算能力．
练习册系列答案
相关题目
2．在复平面内，复数z=（1+i）（2-i）对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
3．近年来空气污染是一个生活中重要的话题，PM2.5就是其中一个重要指标．各省、市、县均要进行实时监测，某市2015年11月的PM2.5浓度统计如图所示．
（1）请完成频率分布表；
（2）专家建议，空气质量为优、良、轻度污染时可正常进行户外活动，中度污染及以上时，取消一切户外活动，在2015年11月份，该市某学校进行了连续两天的户外拔河比赛，求拔河比赛能正常进行的概率．
（3）PM2.5浓度在75以上，空气质量为超标，陶先生在2015年11月份期间曾有两天经过该市，记ξ表示两天中PM2.5检测数据超标的天数，求ξ的分布列及期望．
| 日期 | PM2.5浓度 | 日期 | PM2.5浓度 | 日期 | PM2.5浓度 |
| 11-1 | 137 | 11-11 | 144 | 11-21 | 40 |
| 11-2 | 143 | 11-12 | 166 | 11-22 | 42 |
| 11-3 | 145 | 11-13 | 197 | 11-23 | 35 |
| 11-4 | 193 | 11-14 | 194 | 11-24 | 53 |
| 11-5 | 133 | 11-15 | 219 | 11-25 | 88 |
| 11-6 | 22 | 11-16 | 41 | 11-26 | 29 |
| 11-7 | 22 | 11-17 | 90 | 11-27 | 199 |
| 11-8 | 57 | 11-18 | 46 | 11-28 | 287 |
| 11-9 | 111 | 11-19 | 80 | 11-29 | 291 |
| 11-10 | 134 | 11-20 | 67 | 11-30 | 452 |
| 空气质量指数类别 | PM2.5 24小时浓度均值 | 频数 | 频率 |
| 优 | 0-35 | 4 | $\frac{2}{15}$ |
| 良 | 36-75 | 7 | $\frac{7}{30}$ |
| 轻度污染 | 76-115 | 4 | |
| 中度污染 | 116-150 | 6 | |
| 重度污染 | 151-250 | ||
| 严重污染 | 251-500 | ||
| 合计 | / | 30 | 1 |
（3）PM2.5浓度在75以上，空气质量为超标，陶先生在2015年11月份期间曾有两天经过该市，记ξ表示两天中PM2.5检测数据超标的天数，求ξ的分布列及期望．
20．已知等比数列{an}的首项为1，公比为q（0＜q≤1），它的前n项和为Sn，且Tn=$\frac{{S}_{n}}{{S}_{n+1}}$，求$\underset{lim}{n→∞}$Tn的值．
7．
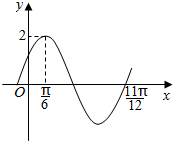已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，丨φ丨＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的解析式为（ ）
已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，丨φ丨＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的解析式为（ ）| A． | f（x）=2sin（x+$\frac{π}{3}$） | B． | f（x）=2sin（2x+$\frac{π}{6}$） | C． | f（x）=2sin（2x-$\frac{π}{6}$） | D． | f（x）=2sin（4x-$\frac{π}{6}$） |