题目内容
已知函数f(x)=x-
-alnx(a∈R)
(1)若f(x)在点(1,f(1))处的切线与圆x2+y2-2y=0相切,求a的值;
(2)是否存在实数a,使得f(x)>0在(1,+∞)上恒成立?如果存在,试求出实数a的取值范围;如果不存在,请说明理由.
| 1 |
| x |
(1)若f(x)在点(1,f(1))处的切线与圆x2+y2-2y=0相切,求a的值;
(2)是否存在实数a,使得f(x)>0在(1,+∞)上恒成立?如果存在,试求出实数a的取值范围;如果不存在,请说明理由.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:分类讨论,导数的概念及应用,导数的综合应用,直线与圆
分析:(1)求出导数,求得在切点处的切线斜率,以及切点,由点斜式方程求得切线方程,求得圆的圆心和半径,由直线和圆相切的条件可得d=r,计算即可得到a;
(2)假设存在实数a,使得f(x)>0在(1,+∞)上恒成立,求出函数的导数,对a讨论,当-2≤a≤2时,当a>2时,当a<-2时,考虑它们的单调性,即可判断a的范围.
(2)假设存在实数a,使得f(x)>0在(1,+∞)上恒成立,求出函数的导数,对a讨论,当-2≤a≤2时,当a>2时,当a<-2时,考虑它们的单调性,即可判断a的范围.
解答:
解:(1)f(x)=x-
-alnx的导数为f′(x)=1+
-
,
即有f(x)在点(1,f(1))处的切线斜率为2-a,
又f(1)=0,
则有f(x)在点(1,f(1))处的切线方程为y=(2-a)(x-1).
圆x2+y2-2y=0的圆心为(0,1),半径为1,
由直线和圆相切可得,
=1,
解得a=2;
(2)假设存在实数a,使得f(x)>0在(1,+∞)上恒成立,
由f′(x)=1+
-
=
,
若△=a2-4≤0,即-2≤a≤2,则f′(x)≥0在(1,+∞)上恒成立,
即有f(x)在(1,+∞)上递增,则f(x)>f(1)=0恒成立;
若△=a2-4>0即a>2或a<-2时,
当a>2时,x2-ax+1=0的两根为x1=
,x2=
.
即有x1<1,x2>1,则在(1,x2)上f(x)递减,在(x2,+∞)上递增,
则f(x)>f(1)=0不恒成立;
当a<-2时,x1<0,x2<0,f(x)在(1,+∞)上递增,则f(x)>f(1)=0恒成立.
综上可得,存在实数a,且当a≤2,使得f(x)>0在(1,+∞)上恒成立.
| 1 |
| x |
| 1 |
| x2 |
| a |
| x |
即有f(x)在点(1,f(1))处的切线斜率为2-a,
又f(1)=0,
则有f(x)在点(1,f(1))处的切线方程为y=(2-a)(x-1).
圆x2+y2-2y=0的圆心为(0,1),半径为1,
由直线和圆相切可得,
| |a-2-1| | ||
|
解得a=2;
(2)假设存在实数a,使得f(x)>0在(1,+∞)上恒成立,
由f′(x)=1+
| 1 |
| x2 |
| a |
| x |
| x2-ax+1 |
| x |
若△=a2-4≤0,即-2≤a≤2,则f′(x)≥0在(1,+∞)上恒成立,
即有f(x)在(1,+∞)上递增,则f(x)>f(1)=0恒成立;
若△=a2-4>0即a>2或a<-2时,
当a>2时,x2-ax+1=0的两根为x1=
a-
| ||
| 2 |
a+
| ||
| 2 |
即有x1<1,x2>1,则在(1,x2)上f(x)递减,在(x2,+∞)上递增,
则f(x)>f(1)=0不恒成立;
当a<-2时,x1<0,x2<0,f(x)在(1,+∞)上递增,则f(x)>f(1)=0恒成立.
综上可得,存在实数a,且当a≤2,使得f(x)>0在(1,+∞)上恒成立.
点评:本题考查导数知识的运用,考查导数的几何意义,函数的单调性,解题的关键是正确求导,合理分类,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 ,当
,当 时,
时, 的函数值均为负值,则实数
的函数值均为负值,则实数 的取值范围是 .
的取值范围是 .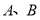 为两个定点,
为两个定点,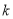 为非零常数,
为非零常数, ,则动点
,则动点 的轨迹为双曲线;
的轨迹为双曲线;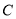 上一定点
上一定点 作圆的动点弦
作圆的动点弦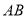 ,
,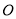 为坐标原点,若
为坐标原点,若 则动点
则动点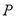 的轨迹为圆;
的轨迹为圆; ,则双曲线
,则双曲线 与
与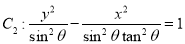 的离心率相同;
的离心率相同;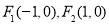 和一动点
和一动点 ,若
,若 ,则点
,则点 的轨迹关于原点对称.
的轨迹关于原点对称.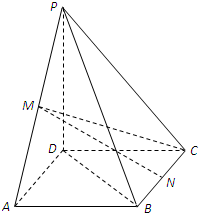 如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别是PA,PB的中点,PD⊥平面ABCD,且PD=AD=
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别是PA,PB的中点,PD⊥平面ABCD,且PD=AD=