题目内容
13.已知f(x)=$\frac{1}{x}$+$\frac{{e}^{x}}{e}$-3,F(x)=lnx+$\frac{{e}^{x}}{e}$-3x+2.(1)判断f(x)在(0,+∞)上的单调性;
(2)判断函数F(x)在(0,+∞)上零点的个数.
分析 (1)求出f(x)的导数,通过解关于导函数的不等式,求出函数的单调区间即可;(2)根据函数的单调性判断出函数F(x)的大致图象,从而判断出函数的零点的个数.
解答 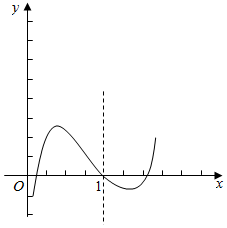 解:(1)f′(x)=-$\frac{1}{{x}^{2}}$+$\frac{{e}^{x}}{e}$=$\frac{{{x}^{2}e}^{x}-e}{{ex}^{2}}$,
解:(1)f′(x)=-$\frac{1}{{x}^{2}}$+$\frac{{e}^{x}}{e}$=$\frac{{{x}^{2}e}^{x}-e}{{ex}^{2}}$,
令f′(x)>0,解得:x>1,令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)递减,在(1,+∞)递增;
(2)F′(x)=f(x)=$\frac{1}{x}$+$\frac{{e}^{x}}{e}$-3,
由(1)得:?x1,x2,满足0<x1<1<x2,
使得f(x)在(0,x1)大于0,在(x1,x2)小于0,在(x2,+∞)大于0,
即F(x)在(0,x1)递增,在(x1,x2)递减,在(x2,+∞)递增,
而F(1)=0,x→0时,F(x)→-∞,x→+∞时,F(x)→+∞
画出函数F(x)的草图,如图示:,
故F(x)的零点有3个.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
4.下列说法正确的是( )
| A. | “p∨q为真”是“p∧q为真”的充分不必要条件 | |
| B. | 若a,b∈[0,1],则不等式a2+b2<$\frac{1}{4}$成立的概率是$\frac{1}{4}$ | |
| C. | 已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | |
| D. | 已知空间直线a,b,c,若a⊥b,b⊥c,则a∥c |
8.在程序框图中,输入N=8,按程序运行后输出的结果是( )


| A. | 6 | B. | 7 | C. | 10 | D. | 12 |
18.已知集合A={x|0≤x≤2},集合B={x|y=$\sqrt{x-1}$},则A∩B=( )
| A. | {x|1<x<2} | B. | {x|1≤x≤2} | C. | {x|1≤x<2} | D. | {x|0≤x≤2} |
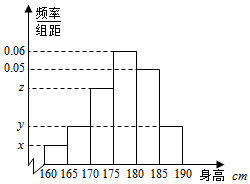 为了了解某中学男生身高,从该校的总共800名男生中抽取40名进行调查,并制成如下频率分布直方图,已知x:y:z=1:2:4.则y的值为0.02.
为了了解某中学男生身高,从该校的总共800名男生中抽取40名进行调查,并制成如下频率分布直方图,已知x:y:z=1:2:4.则y的值为0.02.