题目内容
14.某学校高三年级有两个文科班,四个理科班,现每个班指定1人,对各班的卫生进行检查,若每班只安排一人检查,且文科班学生不检查文科班,理科班学生不检查自己所在的班,则不同安排方法的种数是( )| A. | 48 | B. | 72 | C. | 84 | D. | 168 |
分析 分两步,第一步选2名理科班的学生检查文科班,第二步,理科班检查的方法,需要分三类,根据分步和分类计数原理可得.
解答 解:第一步选2名理科班的学生检查文科班,有A42=12种,
第二步,分三类,第1类,2名文科生检查剩下的2名理科生所在的班级,2名理科生检查另2名理科生所在的班级,有A22A22=4种,
第2类,2名文科生检查去文科班检查的2名理科生所在的班级,剩下的2名理科生互查所在的班级,有A22A11=2种,
第3类,2名文科生一人去检查去文科班检查的2名理科生所在的班级的一个和一人去查剩下的2名理科生其中一个所在的班级,有A21A21A21=8种,
根据分类分步计数原理可得,共有12×(4+2+8)=168种不同安排方法
故选:D.
点评 本题考查了分步和分类计数原理,关键是分类,属于中档题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
4.下列说法正确的是( )
| A. | “p∨q为真”是“p∧q为真”的充分不必要条件 | |
| B. | 若a,b∈[0,1],则不等式a2+b2<$\frac{1}{4}$成立的概率是$\frac{1}{4}$ | |
| C. | 已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | |
| D. | 已知空间直线a,b,c,若a⊥b,b⊥c,则a∥c |
19.从编号为001,002,003,…,300的300个产品中用系统抽样的方法抽取一个样本,已知样本编号从小到大依次为006,018,030,…,则样本中编号排在第11位的是( )
| A. | 102 | B. | 114 | C. | 126 | D. | 138 |
6.若(x+$\frac{a}{{x}^{2}}$)9的二项展开式中含x6项的系数是36,则实数a=( )
| A. | 1 | B. | -1 | C. | $\frac{\sqrt{2}}{2}$ | D. | 4 |
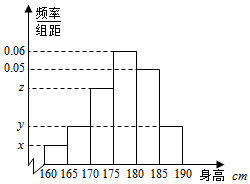 为了了解某中学男生身高,从该校的总共800名男生中抽取40名进行调查,并制成如下频率分布直方图,已知x:y:z=1:2:4.则y的值为0.02.
为了了解某中学男生身高,从该校的总共800名男生中抽取40名进行调查,并制成如下频率分布直方图,已知x:y:z=1:2:4.则y的值为0.02.