题目内容
在平面直角坐标系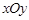 中,以坐标原点
中,以坐标原点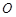 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线 的极坐标方程为
的极坐标方程为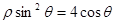 ,直线
,直线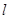 的参数方程为
的参数方程为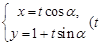 为参数,
为参数,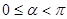 ).
).
(Ⅰ)化曲线 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;
(Ⅱ)若直线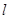 经过点
经过点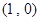 ,求直线
,求直线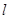 被曲线
被曲线 截得的线段
截得的线段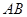 的长.
的长.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)先在方程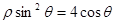 两边同时乘以
两边同时乘以 得
得 ,然后将
,然后将 ,
, 进行代换,边可以得到曲线的直角坐标方程;(Ⅱ)将直线的方程与抛物线方程进行联立,然后利用焦点弦公式
进行代换,边可以得到曲线的直角坐标方程;(Ⅱ)将直线的方程与抛物线方程进行联立,然后利用焦点弦公式 并结合韦达定理可以求出
并结合韦达定理可以求出
试题解析:解法一:(Ⅰ)由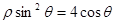 得,
得, ,
,
即曲线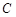 的直角坐标方程为
的直角坐标方程为 . 3分
. 3分
(Ⅱ)由直线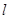 经过点
经过点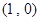 ,得直线
,得直线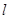 的直角坐标方程是
的直角坐标方程是 ,
,
联立 ,消去
,消去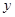 ,得
,得 ,又点
,又点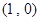 是抛物线的焦点,
是抛物线的焦点,
由抛物线定义,得弦长 . 7分
. 7分
解法二:(Ⅰ)同解法一. 3分
(Ⅱ)由直线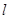 经过点
经过点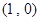 ,得
,得 ,直线
,直线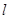 的参数方程为
的参数方程为
将直线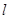 的参数方程代入
的参数方程代入 ,得
,得 ,
,
所以 . 7分
. 7分
考点:极坐标方程、焦点弦

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知椭圆
 (a>b>0)抛物线
(a>b>0)抛物线
 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
 |  | 4 |  | 1 |
 | 2 | 4 |  | 2 |
 的标准方程;
的标准方程;(2)四边形ABCD的顶点在椭圆
 上,且对角线AC、BD过原点O,若
上,且对角线AC、BD过原点O,若 ,
,(i) 求
 的最值.
的最值.(ii) 求四边形ABCD的面积;
 (
(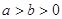 )右顶点与右焦点的距离为
)右顶点与右焦点的距离为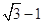 ,短轴长为
,短轴长为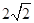 .
.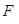 的直线与椭圆分别交于
的直线与椭圆分别交于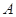 、
、 两点,若三角形
两点,若三角形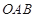 的面积为
的面积为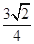 ,求直线
,求直线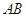 的方程.
的方程. 的上、下顶点分别为
的上、下顶点分别为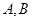 ,点
,点 在椭圆上,且异于点
在椭圆上,且异于点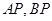 与直线
与直线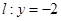 分别交于点
分别交于点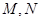 ,
,
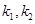 ,求证:
,求证: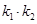 为定值;
为定值;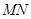 的长的最小值;
的长的最小值;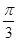 )=-1,曲线C2的极坐标方程为ρ=2
)=-1,曲线C2的极坐标方程为ρ=2 cos(θ-
cos(θ- ).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.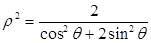 以极点为原点,极轴为
以极点为原点,极轴为 轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.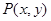 ,求
,求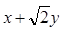 的取值范围;
的取值范围;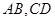 交于点
交于点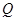 ,且直线
,且直线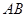 与
与 的倾斜角互补,
的倾斜角互补,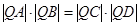 .
. 中,曲线
中,曲线 的参数方程为:
的参数方程为: (
( 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 为极点,以
为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的极坐标方程为:
的极坐标方程为: .
. 是曲线
是曲线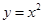 上,A,C关于
上,A,C关于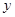 轴对称,BD平行于抛物线在点C处的切线。
轴对称,BD平行于抛物线在点C处的切线。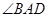 ;
;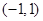 ,四边形ABCD的面积为4,求直线BD的方程。
,四边形ABCD的面积为4,求直线BD的方程。 :
: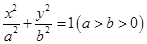 的离心率为
的离心率为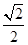 ,左焦点为
,左焦点为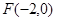 .
. 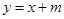 与曲线
与曲线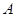 、
、 两点,且线段
两点,且线段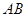 的中点
的中点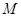 在圆
在圆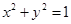 上,求
上,求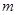 的值.
的值.