题目内容
如图,已知椭圆 的上、下顶点分别为
的上、下顶点分别为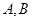 ,点
,点 在椭圆上,且异于点
在椭圆上,且异于点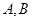 ,直线
,直线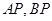 与直线
与直线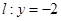 分别交于点
分别交于点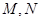 ,
,
(Ⅰ)设直线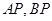 的斜率分别为
的斜率分别为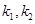 ,求证:
,求证: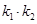 为定值;
为定值;
(Ⅱ)求线段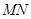 的长的最小值;
的长的最小值;
(Ⅲ)当点 运动时,以
运动时,以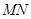 为直径的圆是否经过某定点?请证明你的结论.
为直径的圆是否经过某定点?请证明你的结论.
(Ⅰ)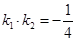 ;(Ⅱ)
;(Ⅱ)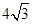 ;(Ⅲ)
;(Ⅲ)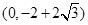 或
或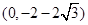 .
.
解析试题分析:(Ⅰ)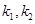 随点
随点 运动而变化,故设点
运动而变化,故设点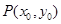 表示
表示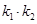 ,进而化简整体消去变量;(Ⅱ)点
,进而化简整体消去变量;(Ⅱ)点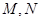 的位置由直线
的位置由直线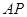 ,
,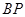 生成,所以可用两直线方程解出交点坐标,求出
生成,所以可用两直线方程解出交点坐标,求出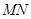 ,它必是
,它必是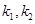 的函数,利用基本不等式求出最小值; (Ⅲ)利用
的函数,利用基本不等式求出最小值; (Ⅲ)利用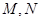 的坐标求出圆的方程,方程必含有参数
的坐标求出圆的方程,方程必含有参数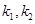 ,消去一个后,利用等式恒成立方法求出圆所过定点坐标.
,消去一个后,利用等式恒成立方法求出圆所过定点坐标.
试题解析:(Ⅰ)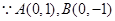 ,令
,令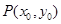 ,则由题设可知
,则由题设可知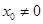 ,
,
∴直线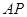 的斜率
的斜率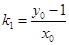 ,
,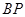 的斜率
的斜率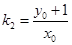 ,又点
,又点 在椭圆上,
在椭圆上,
所以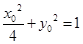 ,(
,(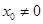 ),从而有
),从而有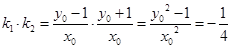 .
.
(Ⅱ)由题设可以得到直线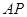 的方程为
的方程为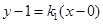 ,
,
直线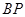 的方程为
的方程为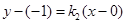 ,
,
由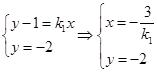 , 由
, 由 ,
,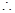 直线
直线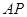 与直线
与直线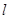 的交点
的交点 ,直线
,直线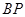 与直线
与直线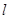 的交点
的交点 .
.
又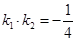 ,
,
等号当且仅当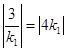 即
即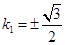 时取到,故线段
时取到,故线段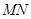 长的最小值是
长的最小值是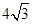 .
.
(Ⅲ)设点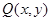 是以
是以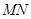 为直径的圆上的任意一点,则
为直径的圆上的任意一点,则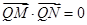 ,故有
,故有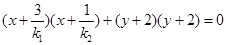 ,又
,又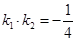 ,所以以
,所以以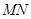 为直径的圆的方程为
为直径的圆的方程为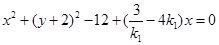 ,令
,令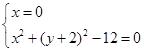 解得
解得 ,
,
以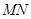 为直径的圆是否经过定点
为直径的圆是否经过定点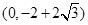 和
和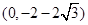 .
.
考点:直线的交点,圆的方程,圆过定点问题,基本不等式的应用.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
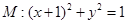 ,圆
,圆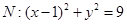 ,动圆
,动圆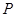 与圆
与圆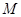 外切并且与圆
外切并且与圆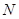 内切,圆心
内切,圆心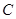 。
。 是与圆
是与圆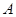 ,
,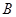 两点,当圆
两点,当圆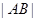 。
。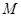 到定点
到定点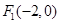 和
和 的距离之和为
的距离之和为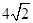 .
. 的方程;
的方程;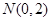 ,过点
,过点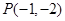 作直线
作直线 ,交椭圆
,交椭圆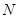 的
的 两点,直线
两点,直线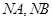 的斜率分别为
的斜率分别为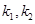 ,证明:
,证明: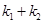 为定值.
为定值.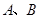 的坐标分别是
的坐标分别是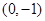 、
、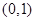 ,直线
,直线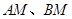 相交于点
相交于点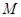 ,且它们的斜率之积为
,且它们的斜率之积为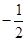 .
.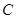 的方程;
的方程;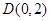 的直线
的直线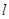 与(1)中的轨迹
与(1)中的轨迹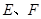 ,试求
,试求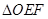 面积的取值范围(
面积的取值范围(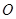 为坐标原点).
为坐标原点).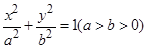 的长轴两端点分别为
的长轴两端点分别为 ,
,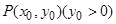 是椭圆上的动点,以
是椭圆上的动点,以 为一边在
为一边在 轴下方作矩形
轴下方作矩形 ,使
,使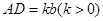 ,
,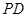 交
交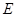 ,
, 交
交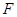 .
.
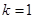 ,且
,且 为椭圆上顶点时,
为椭圆上顶点时,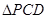 的面积为12,点
的面积为12,点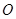 到直线
到直线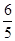 ,求椭圆的方程;
,求椭圆的方程; ,试证明:
,试证明: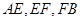 成等比数列.
成等比数列.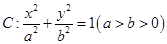 的左右焦点分别为
的左右焦点分别为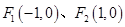 ,且经过点
,且经过点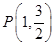 ,
,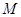 为椭圆上的动点,以
为椭圆上的动点,以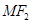 为半径作圆
为半径作圆 的方程;
的方程; 轴有两个交点,求点
轴有两个交点,求点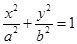 的离心率等于
的离心率等于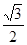 ,点P
,点P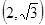 在椭圆上。
在椭圆上。 的方程;
的方程;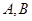 ,过点
,过点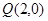 的动直线
的动直线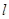 与椭圆
与椭圆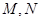 两点,是否存在定直线
两点,是否存在定直线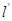 :
: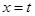 ,使得
,使得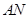 的交点
的交点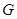 总在直线
总在直线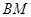 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的 值;若不存在,说明理由.
值;若不存在,说明理由.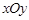 中,以坐标原点
中,以坐标原点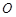 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线 的极坐标方程为
的极坐标方程为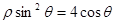 ,直线
,直线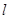 的参数方程为
的参数方程为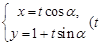 为参数,
为参数,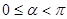 ).
).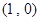 ,求直线
,求直线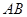 的长.
的长.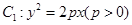 的焦点
的焦点 以及椭圆
以及椭圆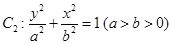 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆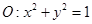 上.
上.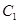 和椭圆
和椭圆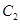 的标准方程;
的标准方程; 两不同点,交
两不同点,交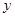 轴于点
轴于点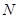 ,已知
,已知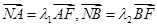 ,求
,求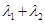 的值;
的值;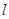 交椭圆
交椭圆 两不同点,
两不同点, 轴的射影分别为
轴的射影分别为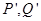 ,
, ,若点
,若点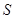 满足
满足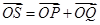 ,证明:点
,证明:点