题目内容
极坐标系中椭圆C的方程为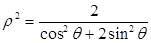 以极点为原点,极轴为
以极点为原点,极轴为 轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(Ⅰ)求该椭圆的直角标方程;若椭圆上任一点坐标为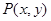 ,求
,求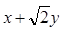 的取值范围;
的取值范围;
(Ⅱ)若椭圆的两条弦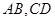 交于点
交于点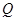 ,且直线
,且直线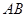 与
与 的倾斜角互补,
的倾斜角互补,
求证: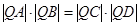 .
.
(Ⅰ) (Ⅱ)详见解析
(Ⅱ)详见解析
解析试题分析:将椭圆的极坐标方程转化为一般标准方程,再利用换元法求范围,利用参数方程代入,计算得到结果.
试题解析:(Ⅰ)该椭圆的直角标方程为 , 2分
, 2分
设 ,
,
所以 的取值范围是
的取值范围是 4分
4分
(Ⅱ)设直线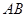 的倾斜角为
的倾斜角为 ,直线
,直线 的倾斜角为
的倾斜角为 ,
,
则直线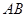 的参数方程为
的参数方程为 (
( 为参数),(5分)
为参数),(5分)
代入 得:
得:
即 7分
7分
同理 9分
9分
所以 (10分)
(10分)
考点:极坐标、参数方程,换元法应用.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
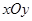 中,点
中,点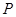 到两点
到两点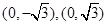 的距离之和等于4,设点
的距离之和等于4,设点 ,直线
,直线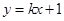 与
与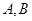 两点.
两点.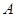 在第一象限,证明当
在第一象限,证明当 时,恒有
时,恒有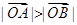 .
.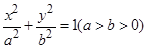 的长轴两端点分别为
的长轴两端点分别为 ,
,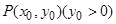 是椭圆上的动点,以
是椭圆上的动点,以 为一边在
为一边在 轴下方作矩形
轴下方作矩形 ,使
,使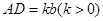 ,
,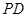 交
交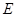 ,
, 交
交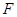 .
.
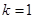 ,且
,且 为椭圆上顶点时,
为椭圆上顶点时,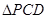 的面积为12,点
的面积为12,点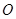 到直线
到直线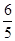 ,求椭圆的方程;
,求椭圆的方程; ,试证明:
,试证明: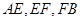 成等比数列.
成等比数列.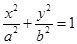 的离心率等于
的离心率等于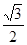 ,点P
,点P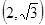 在椭圆上。
在椭圆上。 的方程;
的方程; ,过点
,过点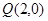 的动直线
的动直线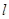 与椭圆
与椭圆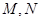 两点,是否存在定直线
两点,是否存在定直线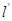 :
: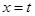 ,使得
,使得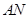 的交点
的交点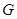 总在直线
总在直线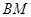 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的 值;若不存在,说明理由.
值;若不存在,说明理由.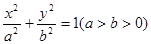 的离心率为
的离心率为 ,
,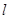 :y=x+2与原点为圆心,以椭圆C的短轴长为直
:y=x+2与原点为圆心,以椭圆C的短轴长为直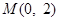 的直线
的直线 与椭圆
与椭圆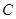 交于
交于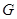 ,
,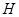 两点.设直线
两点.设直线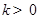 ,在
,在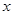 轴上是否存在点
轴上是否存在点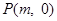 ,使得
,使得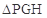 是以GH为底边的等腰三角形. 如果存在,求出实数
是以GH为底边的等腰三角形. 如果存在,求出实数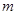 的取值范围,如果不存在,请说明理由.
的取值范围,如果不存在,请说明理由.
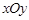 中,以坐标原点
中,以坐标原点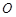 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线 的极坐标方程为
的极坐标方程为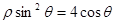 ,直线
,直线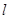 的参数方程为
的参数方程为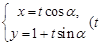 为参数,
为参数,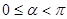 ).
).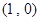 ,求直线
,求直线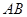 的长.
的长.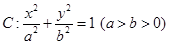 的右焦点为
的右焦点为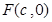 ,上顶点为B,离心率为
,上顶点为B,离心率为 ,圆
,圆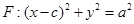 与
与 轴交于
轴交于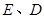 两点
两点 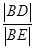 的值;
的值;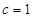 ,过点
,过点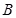 与圆
与圆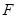 相切的直线
相切的直线 与
与 的另一交点为
的另一交点为 ,求
,求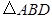 的面积
的面积 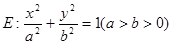 的离心率
的离心率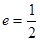 ,
,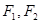 是其左右焦点,点
是其左右焦点,点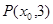 是直线
是直线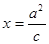 (其中
(其中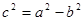 )上一点,且直线
)上一点,且直线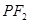 的倾斜角为
的倾斜角为 .
.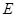 的方程;
的方程; 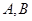 是椭圆
是椭圆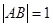 ,求
,求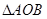 (
(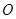 为坐标原点)面积的最小值.
为坐标原点)面积的最小值.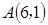 作直线与双曲线
作直线与双曲线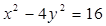 相交于两点
相交于两点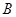 、
、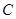 ,且
,且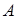 为线段
为线段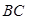 的中点,求这条直线的方程.
的中点,求这条直线的方程.