题目内容
已知椭圆 :
: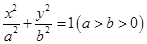 的离心率为
的离心率为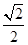 ,左焦点为
,左焦点为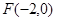 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若直线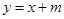 与曲线
与曲线 交于不同的
交于不同的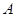 、
、 两点,且线段
两点,且线段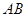 的中点
的中点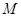 在圆
在圆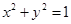 上,求
上,求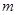 的值.
的值.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)利用离心率和直线与焦点坐标得到两个等量关系,确定椭圆方程;(Ⅱ)利用直线与圆联立,借助韦达定理和中点坐标M在圆上建立等量关系.
试题解析:(Ⅰ)由题意得 ,
, 2分
2分
解得 4分
4分
所以椭圆C的方程为: 6分
6分
(Ⅱ)设点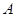 、
、 的坐标分别为
的坐标分别为 ,
, ,线段
,线段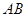 的中点为
的中点为 ,
,
由 ,消去y得
,消去y得 8分
8分
∵ ,∴
,∴ 9分
9分
∴ ,
, 10分
10分
∵点  在圆
在圆 上,∴
上,∴ ,即
,即 13分
13分
考点:1.椭圆方程;2.直线与圆的位置关系.

练习册系列答案
相关题目
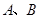 的坐标分别是
的坐标分别是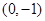 、
、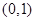 ,直线
,直线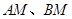 相交于点
相交于点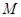 ,且它们的斜率之积为
,且它们的斜率之积为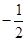 .
.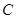 的方程;
的方程;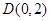 的直线
的直线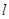 与(1)中的轨迹
与(1)中的轨迹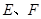 ,试求
,试求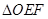 面积的取值范围(
面积的取值范围(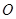 为坐标原点).
为坐标原点).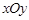 中,以坐标原点
中,以坐标原点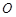 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线 的极坐标方程为
的极坐标方程为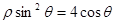 ,直线
,直线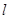 的参数方程为
的参数方程为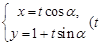 为参数,
为参数,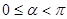 ).
).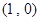 ,求直线
,求直线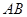 的长.
的长. 的离心率为
的离心率为 ,
, ,
, 为椭圆
为椭圆 的两个焦点,点
的两个焦点,点 在椭圆
在椭圆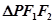 的周长为
的周长为 。
。 与椭圆
与椭圆 、
、 两点,若
两点,若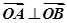 (
( 为坐标原点),求证:直线
为坐标原点),求证:直线 相切.
相切.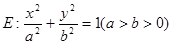 的离心率
的离心率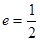 ,
,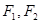 是其左右焦点,点
是其左右焦点,点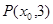 是直线
是直线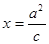 (其中
(其中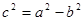 )上一点,且直线
)上一点,且直线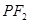 的倾斜角为
的倾斜角为 .
.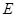 的方程;
的方程; 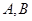 是椭圆
是椭圆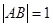 ,求
,求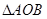 (
(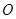 为坐标原点)面积的最小值.
为坐标原点)面积的最小值. 的四个顶点恰好是一边长为2,一内角为
的四个顶点恰好是一边长为2,一内角为 的菱形的四个顶点.
的菱形的四个顶点.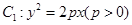 的焦点
的焦点 以及椭圆
以及椭圆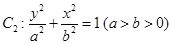 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆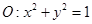 上.
上.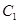 和椭圆
和椭圆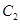 的标准方程;
的标准方程; 两不同点,交
两不同点,交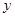 轴于点
轴于点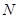 ,已知
,已知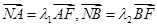 ,求
,求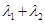 的值;
的值;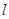 交椭圆
交椭圆 两不同点,
两不同点, 轴的射影分别为
轴的射影分别为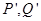 ,
, ,若点
,若点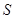 满足
满足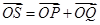 ,证明:点
,证明:点 ,
,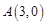 ,动点
,动点 到定点
到定点 距离与到定点
距离与到定点 的距离的比值是
的距离的比值是 .
. 时,记动点
时,记动点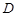 .
. 是圆
是圆 上任意一点,过
上任意一点,过 ,求
,求 的取值范围;
的取值范围; ,
, 是曲线
是曲线 ,有
,有 .试问无论
.试问无论 能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由. 的焦点在
的焦点在 轴上
轴上 的焦距为1,求椭圆
的焦距为1,求椭圆 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 为椭圆
为椭圆 交
交 轴与点
轴与点 ,并且
,并且 ,证明:当
,证明:当 变化时,点
变化时,点