题目内容
以直线x±2y＝0为渐近线，且截直线x－y－3＝0所得弦长为
的双曲线方程为( )
的双曲线方程为( )A． |
B． |
C． |
D． |
D
设双曲线方程为x2－4y2＝λ，
联立方程组
消去y，得3x2－24x＋(36＋λ)＝0.
设直线被双曲线截得的弦为AB，且A(x1，y1)，B(x2，y2)，
那么，
所以
解得λ＝4，故所求双曲线方程是.选D.
联立方程组
消去y，得3x2－24x＋(36＋λ)＝0.
设直线被双曲线截得的弦为AB，且A(x1，y1)，B(x2，y2)，
那么，
所以
解得λ＝4，故所求双曲线方程是
.选D.
练习册系列答案
期末集结号系列答案
相关题目
是双曲线
的左焦点，离心率为
，过
且平行于双曲线渐近线的直线与圆
交于点
，且点
上，则
（ ）
，则双曲线
的（ ）
(a>0，b>0)的两条渐近线与抛物线
(p>0)分别交于O、A、B三点，O为坐标原点．若双曲线的离心率为2，△AOB的面积为
，则p=
C．2 D．3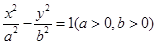
的左焦点，点E是该双曲线的右焦点，过点F且垂直于x轴的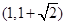
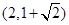
的渐近线方程为
：
与双曲线
：
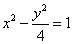有公共的焦点，
，两动点
在双曲线
的右支上，则
的最小值是（ ）
