题目内容
已知F1、F2为双曲线C:x2﹣y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则|PF1|•|PF2|=( )
| A.2 | B.4 | C.6 | D.8 |
B
法1.由余弦定理得
cos∠F1PF2=

∴|PF1|•|PF2|=4
法2; 由焦点三角形面积公式得:
∴|PF1|•|PF2|=4;
故选B.
cos∠F1PF2=


∴|PF1|•|PF2|=4
法2; 由焦点三角形面积公式得:

∴|PF1|•|PF2|=4;
故选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的离心率为( )
的离心率为( )



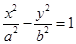 (a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是( )
(a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是( ) )
)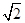 )
)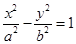 的离心率为
的离心率为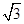 ,则其渐近线方程为( )
,则其渐近线方程为( )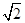 x
x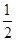 x
x 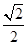 x
x ,0)、F2(
,0)、F2( 满足
满足 ·
· =0,|
=0,| 的双曲线方程为( )
的双曲线方程为( )



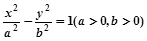 的右焦点为F,若过点F且倾斜角为45°的直线与双曲线的左支没有公共点,则此双曲线离心率的取值范围是( )
的右焦点为F,若过点F且倾斜角为45°的直线与双曲线的左支没有公共点,则此双曲线离心率的取值范围是( )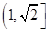

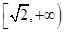
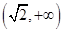
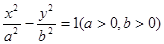 的左、右焦点分别为
的左、右焦点分别为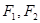 ,若
,若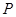 为其上一点,且
为其上一点,且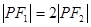 ,
,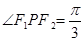 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
 上除顶点外的任意一点,
上除顶点外的任意一点, 、
、 分别是双曲线的左、右焦点,△
分别是双曲线的左、右焦点,△ 的内切圆与边
的内切圆与边 相切于点M,则
相切于点M,则 ( )
( )