题目内容
如果存在满足
+
=1的变量x,y(x>0,y>0),使得x+y-
最得最大值,则m的取值范围是 .
| 1 |
| x |
| m |
| y |
| x2+y2 |
考点:导数在最大值、最小值问题中的应用,基本不等式
专题:不等式的解法及应用
分析:设x=rcosθ,y=rsinθ(r>0,0<θ<
),由
+
=1,可得r=
+
,设f(θ)=x+y-
利用导数研究其单调性极值与最值可得,令f′(θ)=0,解得m=
,画出图形,利用斜率的意义即可得出.
| π |
| 2 |
| 1 |
| x |
| m |
| y |
| 1 |
| cosθ |
| m |
| sinθ |
| x2+y2 |
| cosθ-(-1) |
| sinθ-(-1) |
解答:
解:设x=rcosθ,y=rsinθ(r>0,0<θ<
),
∵
+
=1,∴r=
+
,
∴f(θ)=x+y-
=r(sinθ+cosθ-1)=(
+
)(sinθ+cosθ-1)=1+m+
+
,
f′(θ)=
+
,
令f′(θ)=0,
解得m=
,
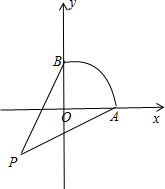
m为动点Q(cosθ,sinθ)到定点P(-1,-1)的斜率,动点Q的轨迹为
的圆,在第一象限,
由图可知:斜率的最大值为kPB=2,最小值为kPA=
,
∴m的范围为(
,2).
故答案为:(
,2).
| π |
| 2 |

∵
| 1 |
| x |
| m |
| y |
| 1 |
| cosθ |
| m |
| sinθ |
∴f(θ)=x+y-
| x2+y2 |
=r(sinθ+cosθ-1)=(
| 1 |
| cosθ |
| m |
| sinθ |
| sinθ-1 |
| cosθ |
| m(cosθ-1) |
| sinθ |
f′(θ)=
| cos2θ+cosθ(sinθ-1) |
| cos2θ |
| -msin2θ-(mcosθ-m)cosθ |
| sin2θ |
令f′(θ)=0,
解得m=
| cosθ-(-1) |
| sinθ-(-1) |
m为动点Q(cosθ,sinθ)到定点P(-1,-1)的斜率,动点Q的轨迹为
| 1 |
| 4 |
由图可知:斜率的最大值为kPB=2,最小值为kPA=
| 1 |
| 2 |
∴m的范围为(
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题考查了通过三角函数代换利用导数研究函数的单调性极值最值转化为斜率的计算,考察了数形结合的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )


| A、12+π | B、8+π |
| C、12-π | D、6-π |
 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图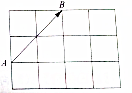 如图所示是4×3的矩形(每个小方格都是单位正方形),在起点和中点都在小方格的顶点处的向量中,试问:
如图所示是4×3的矩形(每个小方格都是单位正方形),在起点和中点都在小方格的顶点处的向量中,试问: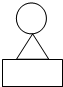 幼儿园的一个小朋友正在给一个圆、一个三角形和一个长方形着色,有红,蓝两种颜色可供选择,对于每一个图形,他都随机地选择一种颜色涂上.
幼儿园的一个小朋友正在给一个圆、一个三角形和一个长方形着色,有红,蓝两种颜色可供选择,对于每一个图形,他都随机地选择一种颜色涂上.