题目内容
设集合A={3，m2}、B={1，3，2m-1}，若A?B，则实数m= ．
考点：子集与真子集
专题：计算题
分析：根据两个集合之间的关系，分m2=2m-1和m2=1两种情况讨论解答，同时要验证元素的互异性．
解答：
解：∵A?B，集合B={1，3，2m-1 }，集合A={ 3，m2 }，
∴当m2=2m-1⇒m=1，不满足集合的性质；
当m2=1⇒m=±1，m=-1时，A={3，1}，B={1，3，-3}，满足集合的性质．
综上m=-1．
故答案是-1．
∴当m2=2m-1⇒m=1，不满足集合的性质；
当m2=1⇒m=±1，m=-1时，A={3，1}，B={1，3，-3}，满足集合的性质．
综上m=-1．
故答案是-1．
点评：本题考查了集合的包含关系的应用，要注意验证集合中元素的互异性．
练习册系列答案
阅读快车系列答案
相关题目
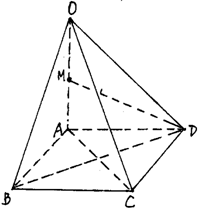如图，在四棱锥O-ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA=2，M为OA中点．
如图，在平行六面体ABCD-A1B1C1D1中，E，H分别是AA1、BB1的中点，求证：