题目内容
17.将不超过30的正整数分成A、B、C三个集合,分别表示可被3整除的数、被3除余1的数、被3除余2的数.请分别用两种方法表示集合A、B、C.分析 利用列举法、描述法、文恩图法,可得结论.
解答 解:A={3,6,9,12,15,18,21,24,27,30}={x|x=3k,k∈N,1≤k≤10},
B={1,4,7,10,13,16,19,22,25,28}={x|x=3k-2,k∈N,1≤k≤10},
C={2,5,8,11,14,17,20,23,26,29}={x|x=3k-1,k∈N,1≤k≤10}
点评 本题考查集合的表示,掌握列举法、描述法、文恩图法是关键.

练习册系列答案
相关题目
7.关于x的方程x2-x•cosA•cosB-cos2$\frac{C}{2}$=0有一个根为1,则△ABC一定是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 钝角三角形 |
5.直线l与平面α有公共点,则有( )
| A. | l∥α | B. | l?α | C. | l与α相交 | D. | l?α或l与α相交 |
12.已知函数$f(x)=\left\{\begin{array}{l}a{x^2}+1,({x≥0})\\(a+3){e^{ax}},({x<0})\end{array}\right.$为R上的单调函数,则实数a的取值范围是( )
| A. | [-1,0) | B. | (0,+∞) | C. | [-2,0) | D. | (-∞,-2) |
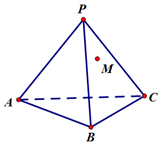 如图,正三棱锥P-ABC,已知AB=2,PA=3
如图,正三棱锥P-ABC,已知AB=2,PA=3