题目内容
20.设空间四边形ABCD中,对角线BD=6cm,且∠BAD=∠BCD=90°,则空间四边形ABCD的外接球的体积为36πcm3.分析 根据题意画出图形,结合图形得出空间四边形ABCD的外接球直径是对角线BD,
求出球的半径,计算其体积即可.
解答  解:如图所示,
解:如图所示,
空间四边形ABCD中,对角线BD=6cm,
且∠BAD=∠BCD=90°,
则空间四边形ABCD的外接球的直径为BD,
∴球的半径为3cm,
其体积为V=$\frac{4π}{3}$•33=36πcm3.
故答案为:36πcm3.
点评 本题考查了空间四边形的外接球的体积计算问题,是基础题.

练习册系列答案
相关题目
11.函数f(x)=x-$\frac{2}{x}$的图象关于( )
| A. | y轴对称 | B. | 原点对称 | C. | 直线y=x对称 | D. | 直线y=-x对称 |
5.直线l与平面α有公共点,则有( )
| A. | l∥α | B. | l?α | C. | l与α相交 | D. | l?α或l与α相交 |
12.已知函数$f(x)=\left\{\begin{array}{l}a{x^2}+1,({x≥0})\\(a+3){e^{ax}},({x<0})\end{array}\right.$为R上的单调函数,则实数a的取值范围是( )
| A. | [-1,0) | B. | (0,+∞) | C. | [-2,0) | D. | (-∞,-2) |
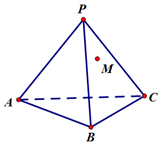 如图,正三棱锥P-ABC,已知AB=2,PA=3
如图,正三棱锥P-ABC,已知AB=2,PA=3