题目内容
设椭圆C:  +
+ =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为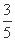 .
.
(1)求C的方程;
(2)求过点(3,0)且斜率为 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.
解:(1)将(0,4)代入C的方程得 =1,
=1,
∴b=4,
又由e= =
=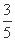 ,得
,得 =
= ,
,
即1- =
= ,
,
∴a=5,
∴C的方程为 +
+ =1.
=1.
(2)过点(3,0)且斜率为 的直线方程为y=
的直线方程为y= (x-3).
(x-3).
设直线与C的交点为A(x1,y1),B(x2,y2),
将直线方程y= (x-3)代入C的方程,
(x-3)代入C的方程,
得 +
+ =1,
=1,
即x2-3x-8=0,
∴x1+x2=3.
设线段AB的中点坐标为(x′,y′),
则x′= =
= ,
,
y′= =
= (x1+x2-6)=-
(x1+x2-6)=-  ,
,
即中点坐标为( ,-
,- ).
).

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
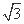 ,1),其中θ∈(0,
,1),其中θ∈(0, 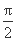 ).
).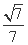 (B)
(B)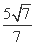 (C)
(C)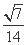 (D)
(D)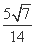
 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( ) (B)
(B) (C)
(C) (D)
(D) 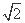 ,
, ).
). +
+ =1上有两个动点P、Q,E(3,0),EP⊥EQ,则
=1上有两个动点P、Q,E(3,0),EP⊥EQ,则 ·
· 的最小值为( )
的最小值为( )
 (B)±
(B)± (D)±
(D)±
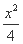 -
- =1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等
=1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等 (B)4
(B)4 (C)3 (D)5
(C)3 (D)5