题目内容

5．g（x）的定义域为R，且满足g（x）+xg′（x）-g′（x）＜0，则y=g（x）的零点个数为（　　）
A．1B．0C．2D．0或2

分析 构造f（x）=（x-1）g（x），则f′（x）＜0，然后根据x与1的关系讨论g（x）的符号．

解答 解：令f（x）=（x-1）g（x）=xg（x）-g（x），则f′（x）=g（x）+xg′（x）-g′（x）＜0，∴f（x）是减函数．
∵f（1）=0，∴当x＜1时，f（x）=（x-1）g（x）＞0，∴g（x）＜0；
当x＞1时，f（x）=（x-1）g（x）＜0，∴g（x）＜0；
∵g（x）+xg′（x）-g′（x）＜0，∴g（1）+g′（1）-g′（1）＜0，即g（1）＜0．
综上，g（x）＜0，∴g（x）无零点．
故选：B．

点评 本题考查了函数的导数与函数单调性的关系，函数单调性的应用，构造合适的函数是解题关键，属于中档题．

练习册系列答案
相关题目
15．集合A={0，2，a}，B={1，a}，若A∪B={0，1，2，4}，则a的值为4．
16．设点P（x0，1），若在以O为圆心的圆O：x2+y2=4上存在一点Q，使∠OPQ=30°，则x0的取值范围是$[-\sqrt{15}，\sqrt{15}]$．
13．已知三个不同的平面α、β、γ和两条不同的直线m、n，有下列五个命题：
①若m∥n，m⊥α，则n⊥α；　　　　　　　　　　　　　②若m⊥α，m⊥β，则α∥β
③若m⊥α，m∥n，n?β，则α⊥β；　　　　　　　　　　　④若m∥α，α∩β=n，则则m∥n
⑤若α⊥γ，β⊥γ，且α∩β=m，则m⊥γ．
其中正确命题的编号是①②③④⑤．
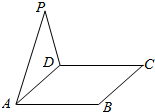20．如图，△ADP为正三角形，四边形ABCD为正方形，平面PAD⊥平面ABCD．M为平面ABCD内的一动点，且满足MP=MC．则点M在正方形ABCD内的轨迹为（O为正方形ABCD的中心）（　　）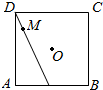
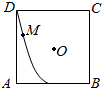
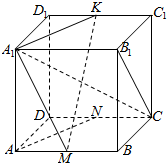A．B．C．D．
10．三棱锥P-ABC三条侧棱两两垂直，三个侧面面积分别为$\frac{{\sqrt{2}}}{2}$，$\frac{{\sqrt{3}}}{2}$，$\frac{{\sqrt{6}}}{2}$，则该三棱锥的外接球表面积为6π．
17．如图所示，M、N、K分别是正方体ABCD-A1B1C1D1的棱AB，CD，C1D1的中点．求证：
（1）AN∥平面A1MK；
（2）MK⊥平面A1B1C．
14．华师一“长飞班”由m位同学组成，学校专门安排n位老师作为指导老师，在该班级的一次活动中，每两位同学之间相互向对方提一个问题，每位同学又向每位指导老师各提出一个问题，并且每位指导老师也向全班提出一个问题，以上所有问题互不相同，这样共提出了51个问题，则m+n=9．
15．已知二次函数y=f（x）的对称轴为x=-2，且过点（0，-8）与（2，4）．
（1）求函数y=f（x）的解析式；
（2）若数列{an}的前n项和Sn=f（n）．求此数列{an}的通项公式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网