题目内容
15.已知二次函数y=f(x)的对称轴为x=-2,且过点(0,-8)与(2,4).(1)求函数y=f(x)的解析式;
(2)若数列{an}的前n项和Sn=f(n).求此数列{an}的通项公式.
分析 (1)运用待定系数法的运用,解方程可得二次函数的解析式;
(2)可得Sn=f(n)=n2+4n-8,讨论n=1,n>1时,an=Sn-Sn-1,化简即可得到所求通项公式.
解答 解:(1)设二次函数f(x)=a(x+2)2+h,
即有-8=4a+h,16a+h=4,
解得a=1,h=-12,
即有f(x)=(x+2)2-12=x2+4x-8;
(2)数列{an}的前n项和Sn=f(n)=n2+4n-8,
n=1时,a1=S1=1+4-8=-3;
n>1时,an=Sn-Sn-1=n2+4n-8-(n-1)2-4(n-1)+8=2n+3,
综上可得,an=$\left\{\begin{array}{l}{-3,n=1}\\{2n+3,n≥2,n∈N}\end{array}\right.$.
点评 本题考查二次函数的解析式的求法,考查数列的通项公式的求法,考查运算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
5.g(x)的定义域为R,且满足g(x)+xg′(x)-g′(x)<0,则y=g(x)的零点个数为( )
| A. | 1 | B. | 0 | C. | 2 | D. | 0或2 |
3.已知一个四棱锥三视图如图所示,若此四棱锥的五个顶点在某个球面上,则该球的表面积为( )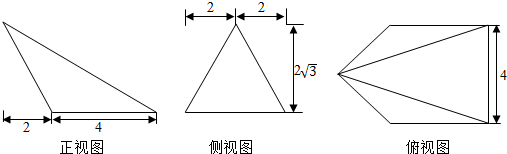

| A. | 48π | B. | 52π | C. | $\frac{172}{3}$π | D. | $\frac{196}{3}$π |
10.若f(x)=x-elnx,0<a<e<b,则下列说法一定正确的是( )
| A. | f(a)<f(b) | B. | f(a)>f(b) | C. | f(a)>f(e) | D. | f(e)>f(b) |
5.下列函数中既是奇函数,又是其定义域上的增函数的是( )
| A. | y=|x| | B. | y=lnx | C. | y=x${\;}^{\frac{1}{3}}$ | D. | y=x-3 |