题目内容
11.已知命题p:实数x满足|x-a|<2,命题q:实数x满足$\frac{2x-1}{x+2}<1$.(1)若命题q为真,求x的取值范围;
(2)若p是q的充分不必要条件,求实数a的取值范围.
分析 (1)通过解不等式求出x的范围即可;(2)分别求出关于p,q的x的范围,得到关于a的不等式组,解出即可.
解答 解:(1)解不等式$\frac{2x-1}{x+2}<1$,得:-2<x<3;
∴命题q为真时:-2<x<3;
(2)解不等式|x-a|<2,得p:-2+a<x<2+a,
若p是q的充分不必要条件,
则$\left\{\begin{array}{l}{-2+a>-2}\\{2+a<3}\end{array}\right.$,解得:0<a<1.
点评 本题考查了充分必要条件,考查集合的包含关系,是一道基础题.

练习册系列答案
相关题目
3.1和9的等比中项是( )
| A. | 5 | B. | 3 | C. | -3 | D. | ±3 |
6.某年青教师近五年内所带班级的数学平均成绩统计数据如表:
(1)利用所给数据,求出平均分与年份之间的回归直线方程$\hat y=bx+a$
(2)利用(1)中所求出的直线方程预测该教师2015年所带班级的数学平均成绩.
参考公式:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 年份x年 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 平均成绩y分 | 97 | 98 | 103 | 108 | 109 |
(2)利用(1)中所求出的直线方程预测该教师2015年所带班级的数学平均成绩.
参考公式:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.
20.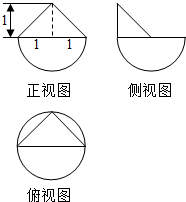 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )
 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A. | 3π+2$\sqrt{2}$-1 | B. | 3π+2$\sqrt{2}$ | C. | 2π+2$\sqrt{2}$-1 | D. | 2π+2$\sqrt{2}$ |
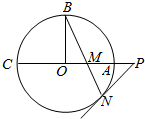 如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P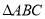 中,
中,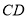 是
是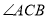 的角平分线,
的角平分线,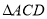 的外接圆交
的外接圆交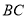 于
于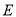 点.
点.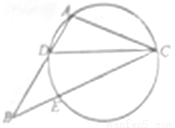
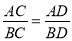 ;
;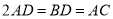 ,求
,求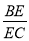 的值.
的值.